Características de Consolidación de las Arcillas Sensibles - Suelos.

Los resultados de una prueba de consolidación en una muestra cuidadosamente extraída de una arcilla de alta sensibilidad (St mayor que 8) se parece a la curva Ku (fig. 3.7). La rama plana inicial de la curva e-log p se convierte en forma relativamente brusca en un tramo inclinado que parece representar un colapso estructural de la arcilla, de manera que un ligero aumento de la presión conduce a una gran disminución en la relación de vacíos. La curva pasa luego por un punto de inflexión y su pendiente disminuye. Si se usa la relación estadística de la ec. 3.2, para determinar la compresibilidad de ese material, el asentamiento calculado es demasiado pequeño. Como el error que se comete está del lado de la inseguridad, los cálculos de los asentamientos deben basarse en pruebas hechas en muestras inalteradas.

Figura 3.7. Curvas e-log p típicas para muestras inalteradas (Ku) y remoldeadas (Kr) de arcilla de alta sensibilidad.

Si se traza una tangente a la parte más inclinada de la curva en su punto de inflexión c, corta la línea e0 en b. La presión correspondiente a b es aproximadamente igual a aquélla en que se produce el colapso. En la mayor parte de las arcillas muy sensibles b queda cuando menos ligeramente a la derecha del punto a, que representa la presión de sobrecarga efectiva po. El incremento de presión b-a puede re- presentar el grado en que ha sido precargado el suelo, o puede representar una resistencia de adherencia que tiene origen en procesos fisicoquímicos subsecuentes a la deposición. En cualquier caso, el incremento representa la presión máxima que puede añadirse al suelo sin excitar los grandes, y a menudo, espectaculares asentamientos asociados a la rama inclinada de la curva. En las zonas en que el subsuelo está formado por arcillas blandas altamente sensibles, como la ciudad de México o partes de Escandinavia, la experiencia ha indicado la necesidad de limitar la presión añadida por un edificio nuevo a solamente una fracción de la resistencia de adherencia.

Las alteraciones producidas durante el muestreo y el manejo de las muestras, pueden enmascarar completamente las características importantes del suelo; las curvas e-log p para arcillas completamente remoldeadas de elevada sensibilidad no son en ningún aspecto diferentes de las arcillas de sensibilidad normal. Aún las arcillas completamente remoldeadas no son tan compresibles como el suelo inalterado a presiones algo superiores a la presión de colapso. Por lo tanto, a diferencia de las estimaciones de los asentamientos en arcillas de sensibilidad normal, las que se hacen en arcillas muy sensibles quedan, si se basan en resultados de pruebas sobre especimenes remoldeados, del lado de la inseguridad. Por lo tanto, son absolutamente indispensables las buenas muestras inalteradas.

Características de Consolidación de los Depósitos Preconsolidados - Suelos.

El diagrama e-Iog p para una archa típica preconsolidada se muestra en la fig. 3.6. Se supone que la muestra se ha tomado con la alteración mínima; además, que en una etapa avanzada de la prueba, la muestra ha sido descargada y vuelto a cargar.

El punto a representa la relación de vacíos inicial de la muestra y la presión efectiva que actuaba en ella antes de extraerla del terreno. Cuando se coloca la muestra en el consolidómetro anegada en agua, es probable, que bajo las pequeñas presiones aplicadas inicialmente, tienda a expanderse. Se acostumbra evitar esta expansión aumentando rápidamente la carga. Así, la primera parte de la curva e-log p usualmente es casi plana; es probable que pase ligeramente abajo del punto a, mientras que la curva de campo debe pasar por l.

El punto a’ corresponde a la relación de vacíos e y a la presión po’ de la arcilla en el campo, cuando el estrato estaba bajo su carga máxima. Por algún proceso, como la erosión, la presión se redujo, y la relación de vacíos aumentó ligeramente por expansión hasta llegar al presente estado, representado por a. (En la figura se desprecia la pequeña expansión que se ha mencionado.) La curva de campo debe pasar cerca de a’, porque antes de la erosión, la relación de campo tendría que haber sido representada por a’f. No se puede construir esta curva con precisión, porque la presion po’ correspondiente al punto a’ ya no se conoce; la presión actual de la sobrecarga es solamente po. Sin embargo, se advierte que la curva Ku para presiones mayores que po consiste con frecuencia de dos segmentos muy diferentes parecidos a los segmentos de la curva m’n en la fig. 3.2. Por analogía con el comportamiento del material remoldeado sujeto a descarga y recompresión, se puede concluir que el primer segmento de Ku (fig. 3.6), a una presión mayor que po, es una curva de recompresión, mientras que el segundo tiene la pendiente de la curva virgen. El quiebre entre los dos segmientos debería, por lo tanto, corresponder a la presión de preconsolidación  po’ y podría estimarse por el procedimiento de A. Casagrande. Además, la pendiente del tramo de recompresión de la curva debe ser similar a la del tramo de recompresión n’g (fig. 3.6). 

Figura 3.6. Curva e-log p (Ku) para una muestra inalterada de una arcilla preconsolidada y reconstrucción de la relación de campo (K). 

Estas consideraciones sugieren el siguiente procedimiento para obtener de manera aproximada, la curva e-log p que corresponde a las condiciones de campo para un material preconsolidado. La prueba de consolidación debe efectuarse en la mejor muestra que pueda obtenerse. Después de aumentar la presión suficientemente como para definir la rama virgen de la curva e-log p, debe efectuarse un ciclo de descarga y recompresión. La presión de preconsolidación puede obtenerse por el procedimiento de A. Casagrande. Luego se haría un bosquejo de la curva de campo de la cual pueden estimarse los asentamientos, empezando en el punto a, y continuando en una dirección paralela a la curva de recompresión  n’g hasta un punto situado aproximadamente a la mitad de la abscisa de Po’. Luego se dirige la curva hacia el punto f, de manera que siga la forma de Ku. Este procedimiento depende del criterio de quien trabaja, pero conduce a resultados razonables. El asentamiento correspondiente a la presión comprendida entre la de sobrecarga actual y la de preconsolidación puede calcularse por medio de la ec. 3.3, pero el valor de Δe debe determinarse de la curva de campo K previamente dibujada (fig. 3.6).

Si no se identifica que la arcilla ha sido preconsolidada y se basa el cálculo de un asentamiento en af, el asentamiento calculado será muy grande. El cambio Δen en la relación de vacíos calculado para un aumento de presión Δp es probable que sea de 4 a 10 veces mayor que el cambio real Δep siempre que Δp no sea mayor de aproximadamente la mitad de po’ - po. Al aproximarse Δo a po’ - po, el error se hace menor.

En los problemas prácticos, el aspecto más importante es poder reconocer si una arcilla ha sido o no preconsolidada. Casi seguramente lo será si la humedad natural se aproxima más al límite plástico que al límite líquido. Además, ejecutando una prueba de consolidación en una muestra tomada cuidadosamente, con frecuencia se obtienen los datos necesarios para decidir al respecto. En la fig. 3.4, se puede advertir que la prolongación hacia arriba de la parte recta de Ku corta la línea e = e0 en el punto b, que está situado a la izquierda del punto a. Esto se cumple siempre en una arcilla normalmente consolidada de sensibilidad normal. Por otra parte, en la fig. 3.6, que se refiere a una arcilla preconsolidada de sensibilidad normal, b está situado al lado derecho de a. Desafortunadamente, la influencia de la alteración tiende, desalojando b a la izquierda, a destruir las evidencias de la preconsolidación. Por lo tanto, si hay probabilidades de que un depósito de arcilla pueda ser preconsolidado y se van a obtener muestras para las pruebas de consolidación, deberán de usarse las mejores técnicas posibles de muestreo. En el art. 4.8 se estudiará otro procedimiento más para investigar el estado de preconsolidacion de una arcilla blanda sedimentaria.

Las arcillas preconsolidadas abundan. Muchos depósitos estuvieron en alguna época sujetos al peso de capas de suelo sobreyacentes que subsecuentemente fueron eliminadas por la erosión. En algunos casos el hielo glacial cubrió y consolidó las capas de suelo inferiores; cuando el hielo se fundió, los depósitos quedaron sobreconsolidados con respecto a la presión que siguió actuando. La superficie de muchos depósitos, especialmente en las llanuras de inundación, estuvo expuesta durante su deposición, sufriendo evaporación y desecación. Los esfuerzos de contracción deben haber sido grandes comparados con las presiones efectivas de sobrecarga actuales y es probable que esos depósitos contengan capas o lentes de arcillas preconsolidadas. El descenso durante largo tiempo de los niveles freáticos producido por bombeo o por las actividades de construcción, puede haber inducido consolidación y precargado la arcilla, con respecto a las condiciones que existieron después del restablecimiento de los niveles freáticos. Para determinar la posibilidad o el grado de preconsolidación en un lugar, las consideraciones históricas y geológicas pueden dar valiosos datos.

Cálculo del Asentamiento - Suelos.

En la fig 3.5a, se muestra una sección transversal de un manto de arcilla de espesor H, quedando la mitad de su espesor situado a la profundidad  D, abajo de la superficie original del terreno. La presión efectiva original en el punto A es igual a Po, y el aumento de presión es Δp. La relación de vacíos inicial de la arcilla, es e0.

La fig. 3.5b, muestra un elemento prismático que contiene al punto A. Puede suponerse que el elemento consiste de materia sólida, que tiene una altura igual a la unidad y un volumen de yacios con una altura adicional equivalente a e. La altura total del elemento es, por lo tanto, 1 + e0.

Si la relación de vados disminuye una cantidad te debido a la consolidación, la deformación unitaria del elemento es Δe /(1 + e0). Suponiendo que esta deformación unitaria es constante en todo el espesor del estrato de ardua, la disminución de espesor del manto, o el asentamiento S arriba del punto A, lo da la ecuación: 

Figura 3.5 a) Sección a través de un manto de arcilla compresible. b) Compresion de un elemento del manto.

Esta ecuación es general y puede usarse para calcular el asentamiento, siempre que se conozcan la relación de vacíos inicial y su cambio. Si la arcilla esta normalmente consolidada, de acuerdo con la ec. 3.1, 

Sustituyendo esta cantidad en la ec. 3.3, se encuentra la siguiente expresión para el asentamiento de la superficie del terreno arriba del punto A, debido a la consolidación de un manto normalmente consolidado de espesor H: 

Características de la Consolidación de los Depósitos Normalmente Consolidados - Suelos.

En el campo, la compresibilidad de una arcilla puede investigarse haciendo pruebas de consolidación en muestras extraídas de manera que su estado se altere lo menos posible. Deben reconocerse dos condiciones diferentes de importancia práctica, que son: si el estrato del que se tomó la muestra está normalmente cargado o si está preconsolidado. Se dice que un estrato está normalmente consolidado, si nunca han actuado en él presiones verticales mayores que las existentes en la actualidad. Por otra parte, un estrato pre o sobreconsolidado, en alguna época de su historia estuvo sujeto a presiones verticales mayores que las que ahora están en actividad.

En la fig. 3.4, se muestra una curva típica e-log p de una muestra inalterada de una arcilla de baja sensibilidad normalmente consolidada. La curva se señala con Ku. Al igual que la porción m’n de la curva e-log p de la fig. 3.2, consta normalmente de dos ramas: de una porción inicial relativamente plana y de otra inclinada casi recta. Para efectos de comparación, Kr, representa los resultados de una prueba en el mismo material después de remoldearlo con una humedad cercana al límite líquido. La porción inferior de Kr, casi recta, tiene una pendiente menor que la de Ku.

Las coordenadas del punto a (fig. 3.4) representan la relación de vacíos y la presión efectiva correspondiente al estado de la arcilla en el campo. Cuando se extrae una muestra empleando las mejores técnicas, la humedad de la arcilla no aumenta significativamente. Por tanto, la relación de vacíos e0 al principio de la prueba es prácticamente idéntica a la que tiene la arcila en el terreno. Cuando la presión en la muestra llega a po, la curva e-log p debe pasar por el punto a, a menos que las condiciones de la prueba difieran en alguna manera de las del campo. En realidad, K pasa siempre abajo del punto a, porque aun las mejores muestras resultan un poco alteradas.

Figura 3.4. Curvas típicas e-log p para muestras inalteradas (Ku) renioldeadas (Kr) de ardua normalmente consolidada de baja sensibilidad. 

Lo que importa al ingeniero es la curva e-log p de la arcilla en el campo, no en el laboratorio. Por lo tanto, necesita disponer de algún procedimiento para extrapolar los resultados de las pruebas de laboratorio a las condiciones representativas en el campo. Un procedimiento para lograrlo puede elaborarse tomando como base la comparación de las curvas Ku y Kr. Se ha observado (Schmertmann, 1955) en muchas arcillas, que las prolongaciones de las porciones inferiores rectas de las curvas Ku y Kr se cortan en un punto f correspondiente a una relación de vacíos aproximadamente igual a O.4e0. Las prolongaciones de las curvas e-log p de las muestras con grados de alteración intermedios también pasan por el punto f o muy cerca del mismo. Por tanto, es razonable suponer que la relación de campo e-log p es aproximadamente una línea recta K que se extiende de a a f.

Si se sabe que un depósito de arcilla está normalmente consolidado, el valor de Po puede calcularse conociendo la humedad, el peso volumétrico de los sólidos, y el grado de saturación de los estratos sobreyacentes, siempre que se conozca la posición del nivel del agua freática. La relación de vacíos inicial de la arcilla también puede calcular- se fácilmente. Por lo tanto, pueden determinarse las coordenadas del punto a. Los procedimientos para calcular Po y € se estudiaron en los arts. 1.6 y 2.4.

El punto f se puede determinar ejecutando una prueba de consolidación en una muestra inalterada o incluso en una muestra parcialmente alterada, Los puntos a y f pueden unirse con una línea recta para determinar la relacion de campo K en la que puede basarse el cálculo del asentamiento.

A la pendiente de K en el diagrama semilogarítmico se le llama índice de compresión Ce, definido por la ecuación: 

 

El valor numérico de Ce, puede determinarse fácilmente del diagrama. Si e1 corresponde a cualquier presión arbitraria P1 y C2 a la presión P2 =  10p1, entonces Ce = e1 -  e2.

Se ha descubierto (Skempton, 1944) que Ce, está íntimamente relacionado al límite liquido de las arcillas sedimentarias normalmente consolidades. La relación entre las dos cantidades es aproximadamente: 

en la que wL  se expresa como porcentaje. La ec. 3.2 es de gran importancia práctica porque permite calcular el asentamiento aproximado de una estructura construida sobre un depósito de arcilla sedimentaria poco sensible normalmente consolidada, si solamente se conoce el límite líquido, aun cuando no se hayan efectuado pruebas de consolidación.

Pruebas de Consolidación en Arcillas Remoldeadas.

Las relaciones entre la presión vertical, el asentamiento y el tiempo, se investigan en el laboratorio por medio de una prueba de compresión confinada, llamada también prueba edométrica o de consolidación edométrica. Durante la prueba, la muestra está completamente confinada por un anillo metálico (fig. 3.1). La carga se aplica a las caras superior e inferior del espécimen a través de dos piedras porosas, que permiten que el agua entre o salga de la arcilla. La deformación se mide por medio de un micrómetro de carátula.

La presión p se aplica por etapas. Después de cada incremento se mantiene la carga constante hasta que la deformación prácticamente cesa. Esto requiere usualmente varias horas, aún para un espécimen que tenga un espesor tan pequeño como de 19 mm, porque la deformación se produce solamente con la rapidez que permite el agua al salir de la arcilla. Cuando la rapidez de la deformación bajo una presión dada se ha reducido hasta ser muy pequeña, se aplica un nuevo incremento y el procedimiento se repite. 

Figura 3.1 Aparato para la prueba de consolidación (Consolidómetro).

Los resultados se presentan gráficamente con una curva que relaciona la oquedad final correspondiente a cada incremento de presión con el valor de dicha presión. Es conveniente dibujar la presión a una escala logarítmica. El diagrama se conoce entonces como curva e-log p o curva de compresibilidad.

Como introducción a las características de las curvas e-log p para las arcillas de sedimentación natural, se considerarán primero los resultados de una prueba de consolidación en una muestra completamente remoldeada en el laboratorio con una humedad cercana al límite líquido. Cuando las relaciones de vacíos son elevadas, la curva es cóncava hacia abajo pero, como lo muestra el segmento km (fig. 3.2), pronto toma la forma de una línea casi recta. La porción casi recta de la curva se denomina línea de consolidación virgen o rama virgen. Si la carga se interrumpe a una presión Po’ correspondiente al punto m, y luego se hace disminuir en decrementos sucesivos, la muestra se expande, como lo indica la curva de descarga mm’. Si se reanuda el proceso de carga, la parte inicial de la curva de recomprensión queda ligeramente arriba de la curva de descarga. Luego, la curva de recomprensión se dobla hacia abajo en forma relativamente brusca, a una presión cercana a Po’, pasa debajo del punto m y se aproxima a la prolongación de la rama virgen. Si a una presiono se descarga y carga nuevamente la muestra, se obtiene otra curva de rebote (nn’) y otra curva de recompresión; las pendientes de estas curvas son aproximadamente iguales a las determinadas anteriormente. Si la presión se aumenta más allá de Po” la curva e-log p de nuevo se dobla bruscamente hacia abajo aproximándose a la rama virgen. Al aumentar más la presión, la curva virgen tiende a convarse ligeramente hacia arriba. 

Figura 3.2  Curva típica e-log p para arcilla remoldeada cerca del limite liquido.

Cuando la muestra está en el estado representado por m’ se dice que esta reconsolidada o sobreconsolidada, porque previamente ha sido consolidada bajo una presión Po’ mayor que la presión Ps, bajo la cual está ahora en equilibrio. El valor Po’ se conoce como carga o presión de preconsolidación. El grado de preconsolidación se mide por la relación po’/ps, conocida como relación de preconsolidación. Es evidente que el quiebre en la curva m n esta íntimamente relacionado a la magnitud de la presión de preconsolidación. 

Se ha ideado un procedimiento gráfico útil (A. Casa- grande, 1936) para estimar el valor de Po’ si solamente se dispone de la curva m’n. Este procedimiento se ilustra en la fig. 3.3.

Para seguir este procedimiento, se elige a ojo el punto c de curvatura máxima de la curva e-Iog p. De c, se traza una tangente a la curva y asimismo, una línea horizontal. Se bisecta luego el ángulo entre estas dos líneas. El punto de intersección de esta bisectriz con la prolongación hacia arriba de una tangente a la parte recta de la curva se representa por d. La abscisa de d corresponde a la presión Po’.

Las presiones Po’ y Ps son esfuerzos efectivos, ya que las relaciones respectivas de vacíos se determinan después de que la muestra ha quedado en equilibrio y el agua ya no tiende a ser expulsada o absorbida. Sin embargo, para simplificar, las barras que indican esfuerzos efectivos, O’ y 8, se omiten, a menos que su omisión produzca confusión. 

Figura 3.3. Construcción grafica para la determinación de la presión de preconsolidación po’ de la curva e-log p (según Casagrande. 1936).

Significado de las Características Esfuerzo - Deformación de los Suelos.

Las características esfuerzo-deformación de un suelo o de una roca, determinan el asentamiento que una estructura dada puede experimentar. En algunos casos, también puede servir como una indicación de las dificultades de construcción que pueden surgir durante la excavación dentro de las masas de suelo.

Los asentamientos de las estructuras construidas sobre mantos de ardua blanda, que algunas veces están enterrados profundamente, debajo de materiales más resistentes y menos compresibles, pueden producirse lentamente y alcanzar grandes magnitudes. Debido al retraso que existe entre el final de la construcción y la aparición de las grietas, en un tiempo el origen de estos asentamientos se consideró misterioso. Los primeros intentos exitosos para explicar el fenómeno sobre una base científica fueron realizados por Terzaghi en
1919.

Los estudios de Terzaghi se referían a la magnitud y velocidad del asentamiento originado en un manto de arcilla al que se le impedía moverse lateralmente y con posibilidades de expulsar el agua hacia arriba o hacia abajo cuando las partículas tendían a juntarse. En muchos casos, estas condiciones aparecen en la práctica.

Por esta razón, y porque la comprensión de los fenómenos es básica para la solución de problemas prácticos más complicados, el estudio del comportamiento de los diferentes suelos cuando se sujetan a esfuerzos, está precedido por un estudio de la consolidación unidimensional de las arcillas saturadas.

Filtración y Redes de Flujo - Suelos.

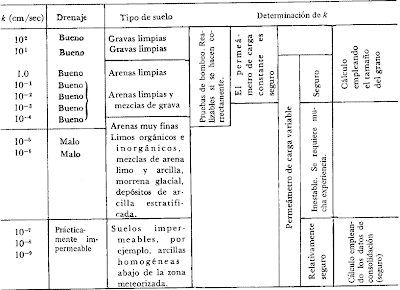
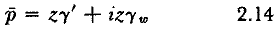Las trayectorias del flujo del agua a través de los suelos reales y las correspondientes presiones de poro son extremadamente complejas, debido a la manera errática en la que es probable que varíe de punto a punto y en diferentes direcciones la permeabilidad. Por lo tanto, los análisis exactos de problemas tan comunes, como el efecto de un sistema de desagüe o el flujo bajo una ataguía dentro de la excavación para la pila de un puente rara vez son posibles. Sin embargo, a pesar de las complejidades de los problemas reales, el ingeniero puede mejorar bastante su criterio con respecto a la filtración y sus efectos, estudiando el flujo en condiciones sencillas esquematizadas.

Por ejemplo, considérese el flujo de agua a través de un material permeable (fig. 2.8a) en el que se ha hincado una tablestaca. Se supone que la permeabilidad del suelo es la misma en todos los puntos y que es igual en todas las direcciones; además, la tablestaca y el manto de roca que está debajo del suelo se consideran completamente impermeables. Se acepta como válida la ley de Darcy, y asimismo que tanto el suelo como el agua son incompresibles.

El agua que entra al suelo aguas arriba del tablestacado, se mueve hacia la superficie del terreno aguas abajo siguiendo trayectorias curvas regulares, como AB (fig. 2.8a), que se conocen con el nombre de lineas de flujo. La circulación es producida por la carga hidráulica h, que impulsa el agua de A a 13. Al moverse una partícula de agua de A hacia B produce un arrastre por fricción en las partículas del suelo; a su vez, este arrastre produce una presión de filtración en la estructura del suelo; la presión de filtración en cualquier punto actúa en la dirección de la línea flujo en ese punto. Debido a esta viscosidad, la carga ha dráulica disminuye continuamente de aguas arriba a aguas abajo a lo largo de cada línea de flujo. En consecuencia, el nivel piezométrico en un punto C tiene un valor intermedio entre los de A y B. Entre los extremos de cualquier otra línea de flujo, como A’B’ la carga hidráulica es también h y existe un punto C’, en el cual el nivel piezométrico es el mismo que en C. Una línea, como LM, que una puntos de igual nivel piezométrico se conoce como línea equipotencial. Si la permeabilidad es constante y la misma en todas direcciones, la teoría demuestra que las líneas equipotenciales deben ser perpendiculares a las líneas de flujo. Esta conclusión permite resolver problemas en los que interviene el movimiento del agua a través de medios porosos, utilizando un procedimiento gráfico, en el que las líneas de flujo y las equipotenciales se dibujan por aproximaciones sucesivas, hasta que se satisfacen las relaciones geométricas necesarias. El diagrama resultante ejemplificado en la fig. 2.8a se conoce como red de flujo.

El primer paso para construir una red de flujo consiste en tomar nota de todas las condiciones de frontera que deben satisfacerse; es decir, determinar si se conocen anticipadamente algunas líneas de flujo o equipotenciales. Por ejemplo, en la fig. 2.8a, la pared formada por el tablestacado mismo constituye una línea de flujo. El agua que entra en el suelo inmediatamente a la izquierda del tablestacado, se mueve verticalmente hacia abajo en dirección de la punta de la tablestacada; pasa a la derecha abajo de la misma, y sube verticalmente a lo largo del paramento de aguas abajo de la propia tablestaca. La superficie del estrato impermeable es también una línea de flujo. El agua que entra a la información infinitamente lejos a la izquierda, fluye a lo largo de esta superficie hasta que ha pasado infinitamente lejos a la derecha. Es evidente que estas dos líneas de flujo marcan las fronteras de la región de flujo. Todas las líneas restantes deben estar si- tuadas entre ellas. Además, debe notarse que la superficie del terreno aguas arriba es una línea equipotencial, porque el nivel del agua en cualquier piezómetro con su ex- tremo inferior en la superficie del terreno, coincidiría con la superficie libre del agua en esa zona. También, la superficie del terreno aguas abajo es una línea equipotencial; el nivel piezométrico coincide con la superficie del agua aguas abajo. Todas las líneas equipotenciales restantes deben localizarse entre estas dos.

Las condiciones de frontera del problema se resumen en la fig. 2.8b. Están representadas por las líneas equipotenciales ab y cd, y por las líneas de flujo bec yfg. La construcción del resto de la red de flujo se comienza haciendo el croquis de un pequeño número de líneas de flujo, quizá solamente dos; cada línea de flujo empieza en ab, y termina en cd. Como ab y cd son líneas equipotenciales, las líneas de flujo deben interceptarlas en ángulo recto. Las líneas de flujo bosquejadas deben ser curvas suaves cuya forma vaya marcando una transición gradual de una línea de flujo de frontera (bec) a la otra (fg). El tanteo inicial puede parecerse al de la fig. 2.8c.

En seguida, se hace el intento de dibujar líneas equipotenciales que cumplan con los requisitos del problema. Estas líneas son también curvas suaves, y deben cruzar a las líneas de flujo en ángulo recto. Además, para simplificar la interpretación de la red de flujo, la separación entre las líneas equipotenciales debe ser tal, que la caída de nivel piezornétrico sea la misma entre cada par de lineas equipotenciales sucesivas. Es también conveniente separar las líneas de flujo, de manera que el gasto en cada canal limitado por dos líneas sucesivas, sea el mismo. Estos dos requisitos pueden satisfacerse haciendo cada área limitada por dos líneas de flujo adyacentes y dos líneas equipotenciales adyacentes, aproximadamente equidimensional. Es decir, las distancias a y b (fig. 2.8d) deben ser iguales. Como recurso para juzgar si un área de lados curvos satisface este criterio, puede inscribirse un círculo en el área. Así, en la fig. 2.8d es evidente que el área P es razonablemente equidimensional, pero que el área Q no satisface los requisitos. 

Figura 2.8. a) Red de flujo por debajo de una ataguía de tablestacas. b) Condiciones de frontera que debe satisfacer la red de flujo. c) Primeras líneas de tanteo para la construcción de la red de flujo. d) Primeras líneas equipotenciales de tanteo para la construcción de la red de flujo. 

 

El primer tanteo de un conjunto de líneas equipotenciales debe dibujarse haciendo un esfuerzo para que las intersecciones resulten en ángulo recto con las líneas de flujo tanto como sea posible, y subdividir el espacio en áreas que puedan diferir entre si en tamaño pero en que cada uno sea equidimensional. Ordinariamente, el primer intento no resulta satisfactorio, pero el estudio del croquis sugerirá las modificaciones apropiadas tanto en las líneas de flujo como en las equipotenciales. Como la forma y posición de cada conjunto de líneas depende de las del otro, comúnmente es necesario hacer una serie de ajustes. Puede adquirirse una gran habilidad para dibujar redes de flujo con la práctica y el estudio de redes bien dibujadas para varias condiciones de frontera. En la fig. 2.9, se muestran varias redes de flujo para problemas relativos a cimentaciones para obras de ingeniería.

Cuando la red de flujo se ha refinado de manera que satisfaga las condiciones de frontera y los criterios geométricos, proporciona la misma información que daría una solución analítica rigurosa del mismo problema. En realidad, con frecuencia las redes de flujo pueden dibujarse fácilmente en problemas demasiado complicados o difíciles para su tratamiento analítico.

Con la red de flujo completa puede determinarse la presión en el agua en cualquier punto de un material permeable. Las condiciones en el punto C, fig. 2.8a, servirán de ejemplo. De acuerdo con la red de flujo, una partícula de agua que siga la trayectoria AB (o cualquier otra línea de flujo), cruzara ocho espacios limitados por líneas equipotenciales sucesivas. Cada espacio representa una caída equipotencial Δh. Si Nd representa el número de caídas equipotenciales a lo largo de cualquier línea de flujo, 

En la fig. 2.8a, Δh = 1/8 h. Cuando el agua llegue al punto C, la carga perdida es 6 Δh, o 6/8h. El nivel piezométrico en C es entonces 6/8 h abajo del nivel del agua aguas arriba, o 2/8 h del nivel aguas abajo. La carga piezométrica en C es, por lo tanto, 

y la presión del agua en C es: 

La presión de poro en C con respecto al nivel de aguas abajo, es la presión disponible en C para impulsar el agua el resto de la distancia a B, y es igual a 2/8 h γw.

El gasto que pasa debajo del tablestacado por unidad de longitud puede calcularse fácilmente. Considérese el gasto Δq a través del área sombreada en la fig. 2.8a. De acuerdo con la ley de Darcy, el gasto es: 

en la que A es el área de la sección transversal del canal de flujo. El canal tiene la anchura a y un espesor unitario en la dirección del muro. Por lo tanto, 

El gradiente hidráulico a través del área sombreada es Δh/a. Sin embargo, 

Si el número de canales de flujo es Nf, el gasto total q por unidad de longitud de muro es: 

El examen de la red de flujo (fig. 2.8a) muestra que la filtración brota en puntos como E o B’ en dirección vertical hacia arriba. Por ejemplo, el gradiente hidráulico hacia arriba en E, puede estimarse como Δh dividida por la distancia DE. Si este gradiente excede del valor crítico (ec. 2.17), el suelo que está inmediatamente aguas abajo del tablestacado se convertirá en movedizo y puede ocurrir una falla. El estudio de las redes de flujo (fig. 2.9) aclarará varias condiciones bajo las cuales pueden producirse condiciones de arena movediza en la práctica, a menos que se tomen precauciones especiales, como la de aumentar la longitud de las tablestacas o añadii bermas, filtros o drenes. 

Figura 2.9. Redes de flujo para varias condiciones. a) Ataguía para la construcción de una pila de puente. b) Excavación para cimentación abajo del nivel del agua frática en arena. c) Desagüe de excavación bombeando el agua valiéndose de coladeras de punta.

En muchos problemas prácticos, el movimiento del agua no está confinado por una frontera artificial superior, sino que tiene lugar abajo de una superficie libre de! agua (figs. 2.9b y 2.9c). La Línea de flujo más alta es entonces una línea de filtración (línea de corriente superior). Como la línea de filtración es una línea de flujo, las líneas equipotenciales que la intercepten deben hacerlo en ángulo recto, pero cada una de estas líneas termina en la línea de filtración. Para satisfacer los requisitos hidráulicos especiales de la línea de filtración, la componente vertical de la distancia entre las terminaciones de dos líneas equipotenciales adyacentes debe ser igual a la caída equipotencial Δh, como se indica en las figs. 2.9b y 2.9c. Para dibujar la red de flujo debe suponerse la posición de la superficie libre del agua, construir una red de flujo tentativa, revisar todos los criterios anteriormente discutidos, así como las condiciones especiales que existan a lo largo de la superficie libre, y revisar el diagrama, hasta que se satisfagan todas las condiciones. La construcción de estas redes de flujo es más difícil que si están fijas las condiciones de frontera superiores, pero los principios son los mismos.

Los procedimientos que se acaban de describir pueden modificarse para tomar en cuenta la estratificación o valores diferentes de la permeabilidad en direcciones horizontales y verticales (A. Casagrande, 1935), Por supuesto, estas condiciones son las que se encuentran con más frecuencia en la práctica, y no las sencillas que se consideraron en los párrafos anteriores. En realidad, con frecuencia el patrón de permeabilidad es tan variable, que ninguna red de flujo puede representar satisfactoriamente las condiciones reales. Sin embargo, pueden lograrse conclusiones prácticas extremadamente útiles del estudio de las trayectorias de flujo en condiciones simplificadas.

Efecto del Congelamiento - Suelos.

Si la temperatura de la superficie del suelo es inferior a la de congelación y si el agua freática no está suficientemente profunda con respecto a la altura del ascenso capilar; el agua, moviéndose hacia arriba continuamente por el efecto capilar y por evaporación y condensación, se acumula y congela, formando lentes de hielo en la parte superior del terreno. Este fenómeno conocido como efecto de congelamiento, es más frecuente en las arenas muy finas y limos, porque estos suelos son capaces de elevar por capilaridad la mayor cantidad de agua en el tiempo más corto (fig. 2.6). Por otra parte, no ocurre en arenas limpias o gravas o suelos de granos mezclados, en los que menos del 3 por ciento de las partículas sean más pequeñas que 0.02 mm. A estos materiales se les designa como inmunes a la congelación. A los suelos arcillosos también les afecta la congelación, pero su baja permeabilidad con frecuencia actúa para impedir la formación de lentes de hielo. Sin embargo, si la arcilla tiene un índice de plasticidad menor que 10 o 12, es muy susceptible al efecto de congelamiento y puede comportarse como un limo. 

En el norte de los Estados Unidos y en Canadá, no es raro que las lentes de hielo alcancen un espesor acumulado de 15 a 46 cm durante un solo invierno. Mismas que ocasionan daños que sufren los pavimentos de las carreteras, porque cuando se funden, el suelo se convierte en un lodo con una capacidad de carga despreciable. El daño puede evitarse quitando todos los materiales muy susceptibles al fenómeno dentro del espesor que penetra el congelamiento, y reemplazándolos con materiales inmunes. Cuando el costo de este tratamiento sea prohibitivo, los materiales inmunes se colocan solamente en la base, directamente bajo la carpeta, y en el resto del pavimento se colocan materiales que sean ligera o moderadamente susceptibles.

Drenaje por Desecación - Suelos.

No es posible drenar suelos finos en un tiempo razonable valiéndose únicamente de la gravedad. Sin embargo, en la naturaleza, el drenaje puede ser efectuado por desecación. Durante este proceso, la humedad se pierde gradualmente por evaporación. Al evaporarse el agua, las partículas de suelo se juntan en posiciones más y más cercanas, debido a la tensión superficial del agua. En el límite de contracción, la resistencia del suelo es suficientemente grande como para soportar las fuerzas de la tensión superficial sin consolidación posterior y. si aumenta la desecación aún más, comienza la invasión de aire. La humedad no disminuye a cero, sano que alcanza un valor en equilibrio con la humedad relativa de la atmósfera. Los suelos arcillosos pueden retener hasta el 7 por ciento de humedad aun en aire seco.

El proceso de desecación aumenta la resistencia de los suelos finos, debido a que al aumentar la tensión en el agua empuja las partículas coloidales poniéndolas más en contacto. Los suelos arcillosos que se han desecado en el campo y luego se saturan, retienen usualmente una gran porción de la resistencia obtenida por la desecación. Las capas de esta arcilla no son raras y pueden proporcionar cimentaciones adecuadas a estructuras ligeras.

Cuando una muestra de suelo fino secada en el aire o en un horno se coloca en agua, el suelo se deslíe. La fuerza de la tensión superficial empuja el agua en los huecos y comprime el aire encerrado en el interior, hasta que la presión excede de la resistencia a la tensión del esqueleto del suelo y ocurre el desleimiento.

Drenaje por Gravedad - Suelos.

Bajando el nivel freático pueden evitarse las dificultades para construir abajo del nivel del agua en depósitos de suelos y puede aumentarse la estabilidad de los mismos. En los materiales de grano grueso, usualmente puede bajarse el nivel freático, drenando el agua a zanjas o galerías, o bombeándola de sumideros o potos. Como la gravedad es la fuerza qu origina la circulación del agua hacia los drenes, el proceso se llama drenaje por gravedad.

Al fluir el agua hacia los drenes, produce presiones de filtración que tienden a mover los granos hacia la salida. Si el suelo es una mezcla de materiales que contiene arena fina o limo, es probable que se deslaven los componentes finos. Lo que puede producir asentamientos o la formación de túneles de erosión en el suelo drenado y, además, obstruir los drenes. Por lo tanto, casi siempre es necesario evitar la migración. Lo que puede lograrse efectivamente cubriendo el material drenado, donde el agua brota, con un material granular más grueso, conocido como filtro, que no impide la salida del agua pero que tiene huecos demasiado pequeños para que los invadan las finas partículas de los materiales que se drenan.

Para que un filtro funcione bien, la curva granulométrica del material que lo constituye debe guardar una relación adecuada con el material que va a protegerse. Los requisitos han sido investigados experimentalmente (Terzaghi, 1922; USBR, 1947). Pueden expresarse por medio de dos relaciones para filtros R 

Tabla 2.2 Requisitos para los tamaños de las partículas en los filtros.

En la tabla 2.2 se proporciona una lista de los valores adecuados de R. Además de satisfacer los requisitos con respecto al 50 por ciento y 15 por ciento de los tamaños, la curva granulométrica del filtro debe tener una forma suave sin quiebres pronunciados y ser sensiblemente paralela a la del suelo que se esta protegiendo.

Los requisitos expuestos en la tabla 2.2 se estudiaron para Las presas de tierra y otras instalaciones permanentes. Para protecciones temporales o usos menos exigentes, los límites granulométricos señalados pueden excederse un poco.

Puede suceder que no sea posible satisfacer los requisitos de la tabla 2.2 con un solo material de filtro, que pueda evitar que se deslaven los finos del suelo protegido, aunque sea capaz de dejar pasar toda el agua que le llegue. Entonces, es necesario construir una serie de filtros que vayan siendo sucesivamente más gruesos conforme el agua se aproxime a la salida. Cada capa del sistema debe satisfacer los requisitos de granulométrica para un filtro con respecto a la capa de material adyacente. Tal sistema se llama un filtro graduado. Asimismo, puede darse el caso de que los requisitos de granulometría de un filtro no sean satisfechos por los materiales de que puede disponerse en la localidad sin lavar, cribar o mezclar, El costo de estas operaciones puede ser considerable. En consecuencia, las capas de los filtros graduados frecuentemente se hacen tan delgadas como sea compatible con la operación del equipo de construcción. Estos filtros tan delgados son vulnerables, especialmente durante la construcción. En la mayor parte de los casos, es preferible usar capas más gruesas de materiales naturales, aunque nada más satisfagan aproximadamente los requisitos. Es difícil evitar la segregación de los materiales de filtro, pero debe mantenerse tan pequeña como sea posible.

No puede extraerse toda el agua de un suelo por procesos gravitacionales. La cantidad que queda en los vacíos es de poca importancia comparada con la rapidez con que puede efectuarse el drenaje. En las arenas limpias y en las gravas, sólo se requieren unas cuantas horas o días para bajar el nivel freático varios metros, mientras que en los suelos limosos pueden necesitarse varias semanas.

Al salir el agua de un suelo grueso, parte del espacio vacío es invadido por aire. Sin embargo, en los suelos finos, el espacio vacío decrece en forma continua y prácticamente no hay invasion de aire hasta alcanzar el límite de contracción. A este proceso se le conoce como drenaje por consolidación.

Fenómenos Capilares - Suelos.

Abajo del nivel del agua freática, los suelos están completa o casi completamente saturados. Arriba de este nivel, el grado de saturación depende de las condiciones climatólogicas, del tamaño de los granos del suelo, y de la distancia al nivel freático. Los suelos gruesos solamente están saturados, aun a elevaciones cercanas al nivel freático, mientras que los suelos finos pueden estar saturados a una considerable altura sobre el mismo. En última instancia, puede definirse el nivel freático corno aquel en el que la presión intersticial es igual a la atmosférica; es decir, uw=O.

Si la gravedad fuera la única fuerza que obrara en el agua en el suelo, el suelo situado arriba del nivel freático estaría siempre completamente seco, excepto durante la filtración resultante de las precipitaciones recientes. Sin embargo, el agua pone de manifiesto la fuerza de la tensión superficial, debida a la atracción entre sus moléculas en una interfase de agua y aire. La tensión superficial combinada con la atracción entre el agua y la mayor parte de las sustancias sólidas, como lo demuestra la facultad del agua para mojar estas sustancias, es una fuerza que tiende a extraer o a retener humedad arriba del nivel freático. Esta fuerza es una manifestación de la capilaridad.

La capilaridad puede demostrarse sumergiendo el extremo inferior de un tubo de vidrio de diámetro pequeño en una vasija que contenga agua. El agua sube en el tubo a una altura que está regida principalmente por el diámetro del tubo y por la limpieza de su superficie interior. A esta altura se le conoce con el nombre de altura de ascensión capilar. Se obtiene en centímetros por medio de la siguiente expresión 

en la que Ts. es la tensión superficial del agua en gramos por centímetro; r el radio del tubo en centímetros; y a el ángulo de contacto entre la superficie del agua y la pared del tubo. Arriba del nivel freático, la presion en el agua es negativa con respecto a la presión atmosférica. Así, a la elevación z arriba del nivel freático, 

Las condiciones del ascenso capilar en una masa de suelo no son estrictamente análogas a las de un tubo de vidrio, debido a que los huecos del suelo tienen diámetros variables. Sin embargo, el diámetro medio de los huecos está relacionado con el promedio del tamaño de los granos, y por lo tanto, con la altura de ascensión capilar. Por ello, como una tosca aproximación de la altura máxima hc (cm) a la que la capilaridad puede elevar el agua en un suelo dado, puede escribirse: 

en la que e es la relación de vacíos; D10 es el diámetro efectivo de Hazen, en centímetros; y C es un coeficiente empírico, que depende de la forma de los granos y de las impurezas de la superficie. En general, C tiene un valor comprendido entre 0.1 y 0.5 cm2.

La altura capilar es mayor para los suelos muy finos, pero la velocidad de ascenso en esos materiales es pequeña, debido a su baja permeabilidad. Así, la elevación capilar que ocurre en un lapso de tiempo determinado, como de 24 hr, es máxima para los materiales en los que el tamaño de los granos es intermedio, como en los limos y las arenas muy finas. La fig. 2.6 muestra la relación entre el tamaño de los granos de un polvo de cuarzo uniforme y su altura de ascensión capilar, en un período de 24 hr.

El agua que sube por capilaridad arriba del nivel freático, alcanza la altura máxima hc sólo en los huecos más pequeños. Unos cuantos huecos grandes pueden detener efectivamente el ascenso capilar en ciertas partes de la masa del suelo. Por lo tanto, la altura hcc (fig. 2.7), a la que el suelo está completamente saturado por capilaridad, es probable que sea considerablemente menor que hc. 

Figura 2.6. Relación entre el tamaño de los granos de polvo de cuarzo uniforme y la altura de la elevación capilar en un periodo de 24 hr (según Atterberg, 1908).

es probable que sea considerablemente menor que hc. Sin embargo, como hay continuidad en el agua, el esfuerzo en ésta se rige en todas partes por la ec. 2.19.

Cierta cantidad del agua de la superficie que se cuela dentro del terreno, no alcanza a llegar al nivel freático, sino que la tensión superficial la sujeta, ya sea en los vados menores, o bien, como anillos rodeando los puntos de contacto entre los granos del suelo. Una cantidad de agua adicional puede ascender arriba del nivel freático debido al proceso de evaporación y condensación. A la humedad de estas fuentes se le conoce con el nombre de humedad de contacto. La tensión superficial en las películas de agua tiende a juntar los granos del suelo y origina la cohesión aparente en las arenas y limos. A esta cohesión se le llama aparente, ya que por inmersión las películas de agua se destruyen y, también la tendencia de los granos a permanecer juntos. 

La cohesión aparente entre los granos de una arena suelta húmeda, inhibe la facultad de los granos de desliz arse entre sí y tomar una configuración más compacta. Como una consecuencia pueden encontrarse terraplenes de material sin compactar en estados notablemente sueltos. Si se les sumerge, la estructura muy suelta sufre un colapso y los granos cambian a un estado aun suelto, pero estable. 

 Figura 2.7. Elevación capilar del agua en arena seca.

Humedad del Suelo, Drenaje y Efecto del Congelamiento.

Agua freática. El nivel que toma el agua en los pozos de observación hechos en los depósitos de suelos se conoce con el nombre de nivel del agua subterránea, superficie libre del agua, o bien nivel freático. Esta definición es válida independientemente del coeficiente de permeabilidad del depósito, aunque la determinación del nivel del agua subterránea en los suelos de grano muy fino, utilizando pozos de observación puede resultar muy imprecisa a menos que se utilicen técnicas especializadas.

En general, el nivel del agua freática abajo de la superficie del terreno de una zona, aun cuando sea tan pequeña como el solar en que se construye un edificio, no es horizontal, sino que forma una superficie suavemente ondulada. El agua que proviene de la lluvia, de la fusión de la nieve, o de fuentes artificiales como el riego, circula continuamente a través del suelo, yendo de las elevaciones mayores a las menores, bajo la influencia de la gravedad. La intersección del nivel del agua freática y una superficie vertical orientada en la dirección de] talud más inclinado del agua freática se denomina frecuentemente línea de filtración (fig. 2.5). La carga piezométrica en cualquier punto P en la línea de filtración 

Figura 2.5. Diagrama que ilustra la línea de filtración.

es cero; es decir, en un tubo piezométrico situado en P, el nivel del agua coincidiría con el nivel de la superficie libre. Similar- mente, la carga piezométrica en Q es cero. La carga hidráulica h en P con respecto a Q, que es la diferencia de niveles piezométricos entre P y Q, es por lo tanto idéntica a la diferencia de elevación real entré los puntos P y Q. Esta relación es una propiedad inherente del nivel del agua freática y de la línea de filtración. Por lo tanto el gradiente hidráulico que impulsa una partícula de agua a lo largo de la línea de filtración, de P a Q es h/1.

Ejemplo: Calucalr la presión efectiva vertical a la mitad de la capa de arena, antes y después del descenso del nivel del agua freática.

En el depósito mostrado en la figura ilustrada, el nivel del agua freática estaba originalmente en la superficie del terreno. A causa del drenaje, el nivel del agua freática descendió a una profundidad de 6.10 m; el grado de saturación de la arena sobre el nivel abatido del agua freática descendió a 20 por ciento. Calcule la presión efectiva vertical a la mitad de la capa de arena, antes y después del descenso del nivel del agua freática. 

Solución. Antes del descenso del nivel del agua freática, la presión efectiva es:

Después del descenso del nivel freático, el peso de la arena húmeda en los 6. 10 m superiores se convierte en: 

Por lo tanto, la presión efectiva a 6.10 m se convierte en: 

Advierta que el descenso del nivel del agua freática aumenta la presión efectiva en la capa de arcilla.

Ejemplos: Calcular la Presión Vertical Efectiva a una Profundidad dada en el deposito.

Calcule la presión vertical efectiva a una profundidad de 9 m en el deposito representado en la figura siguiente.

Solución. Tomando como base los pesos de los materiales sumergidos (ec. 2.12), se puede escribir

 

Presiones de Filtración y Gradiente Hidráulico Crítico - Suelos.

Si el nivel libre del agua se conserva en el borde del recipiente y se baja el depósito, se produce pronto un flujo establecido; de acuerdo con las condiciones ilustradas en la fig. 2.4b. Como el depósito y el tubo flexible se comunican con el fondo del recipiente, la presión intersticial en el fondo del recipiente puede expresarse como:

Esta fórmula representa una disminución de h γw en la presión del agua de los poros, en comparación con la condición mostrada en la fig. 2.4a. Se advierte que esta disminución no puede atribuirse a la velocidad de circulación del agua, debido a que la carga de velocidad v^2/2g es despreciable para velocidades comparables a las más elevadas que se encuentran en los depósitos de suelos naturales. Por lo tanto, la presión total en el fondo del recipiente se determina únicamente por el peso del suelo y del agua que están arriba del mismo. Como resultado, la presión efectiva debe aumentarse en h7 respecto al valor indicado en la fig 2.4a. Por lo tanto, en el plano ab, el aumento proporcional en la presión efectiva es igual a h γw(z/H). El aumento en presión efectiva debido al flujo de agua se conoce con el nombre de presión de filtración. Es el resultado del empuje por fricción del agua corriente sobre los granos del suelo.

Se advierte que la pérdida de carga entre la parte superior del material granular y la profundidad z es hz/H. El gradiente hidráulico correspondiente i es h/H. Por lo tanto, la presión de filtración puede expresarse como izγw, y la presión efectiva a la profundidad Z es:

Si se eleva el depósito arriba del recipiente, de manera que se tenga un flujo ascendente a través del material granular (fig. 24c), la presión intersticial en el fondo del recipiente se aumenta en la cantidad hγw. Por lo tanto, la presión efectiva en el plano ab se reduce a: 

Aumentando el gradiente hidráulico ascendente puede incrementarse la presión de filtracion a zγ’, con lo que la presión efectiva p se hace cero. Esto ocurre cuando: 

El gradiente hidráulico para el cual la presión efectiva se hace cero se denomina gradiente hidráulico crítico ic. Bajo estas condiciones, un suelo sin cohesión no puede soportar ningún peso sobre su superficie. 

Además, al aproximarse el gradiente hidráulico al valor crítico, el suelo se hace mucho más suelto, y aumenta el coeficiente de permeabilidad k. Por tanto, si se hace una excavación en un suelo sin cohesión, bajo el nivel freático, a una profundidad tal que la presión efectiva se reduzca a cero, se observa una agitación visible de los granos del suelo. Este fenómeno se conoce como condición de arena movediza. La mayor  parte de las arenas movedizas son el resultado de esta condición hidráulica especial.

Figura 2.4. Diagrama que ilustra el significado de la presión efectiva y la presión de poro.

Presión Efectiva y Presión de Poro - Suelo.

Definiciones.  El esfuerzo total que obra en cualquier punto de una sección de suelo saturado o de roca, puede dividirse en dos partes. Una de ellas, llamada presión intersticial, presión de poro o esfuerzo neutro uw actúa en el agua y en el sólido con igual intensidad y en todas direcciones. La otra parte, conocida como esfuerzo efectivo p, representa el exceso sobre el esfuerzo neutro, y actúa exclusivamente entre los puntos de contacto de los componentes sólidos. Es decir, 

La experiencia ha demostrado que solamente los esfuerzos efectivos pueden inducir cambios en el volumen de la masa de un suelo. De la misma manera, solamente los esfuerzos efectivos pueden producir resistencia friccionante en los suelos y rocas. Por otra parte, los esfuerzos neutros no pueden por si mismos producir cambios de volumen o bien resistencia friccionante.

A este enunciado se le conoce como principio de los esfuerzos efectivos (Te rzaghi, 1925, 1936; Skempton, 1960). Su importancia es máxima en toda la Mecánica de Suelos y en la Ingeniería de las Cimentaciones.

En forma indirecta, los cambios en los esfuerzos neutrales pueden producir cambios en el volumen del suelo o influir en su resistencia friccionante, pero sólo bajo circunstancias especiales en las que los cambios en esfuerzo neutral produzcan a su vez cambios en los esfuerzos efectivos. La distinción entre los esfuerzos efectivos y los neutrales puede ilustrarse por medio de la fig. 2.4, que muestra un recipiente parcialmente lleno de material granular y completamente lleno de agua. El fondo del recipiente está conectado a un depósito, por medio de un tubo flexible. En la parte a de la figura, el nivel del agua en el depósito es el mismo que en el recipiente, de manera que no hay ningún flujo. En el plano ab, a la profundidad (H1 + z) la presión vertical es:

Donde γw es el peso volumétrico del agua y γsat el del suelo saturado. Puesto que p depende del peso del suelo y el agua suprayacentes, se denomina presión total, Incluye al esfuerzo efectivo p y a la presión de poro uw.

El agua sobre el plano ab tiene continuidad en los vacíos del suelo dentro de la altura z y es una masa continua en la profundidad H1. Por lo tanto, según las leyes de la Hidráulica, la presión de poro uw, en ab será: 

La presión efectiva p es entonces 

La cantidad γsat - γw se conoce como peso volumétrico del suelo sumergido, γ' Por lo tanto, para las condiciones ilustradas en la fig. 2.4a, 

Así, la presión efectiva es independiente de la profundidad H1 del agua arriba del suelo o roca sumergidos.

En las condiciones de la fig. 2.4a no hay flujo de agua a través de los vacíos. En el diagrama de presiones que esta a la derecha de la figura, el cambio de anchura del área sin sombrear representa la variación de la presión en el agua con la profundidad, y el área sombreada representa la distribución de la presión efectiva. Si el nivel del agua en el depósito es diferente del que tiene en el recipiente, entonces se producirá un flujo, y las condiciones son semejantes a las ilustradas en la fig. 2.4b, o 2.4c. Por lo tanto, la ec. 2.10 ya no es válida, y las ecs. 2.11 y 2.12 ya no pueden aplicarse.

-Presiones de Filtración y Gradiente Hidráulico Crítico.

Permeabilidad de las Rocas.

Incluso las rocas más sanas como algunos granitos, mármoles, o pizarras, no pueden ser consideradas como impermeables; sus coeficientes de permeabilidad son de orden de 10^-8 a 10^-10 cm/seg. Sin embargo, la permeabilidad de las formaciones rocosas sanas tiene un interés que apenas sobrepasa al académico para el ingeniero encargado del proyecto y construcción de cimentaciones para puentes o edificios, porque casi la mayor parte de los depósitos de roca contienen canales extraordinariamente permeables, como juntas, planos de sedimentación o cavidades formadas por solución.

Ejemplos de Problemas de Permeabilidad del Suelo: coeficiente de permeabilidad, el valor de K.

1.- Una arena suelta uniforme de granos redondeados tiene un diámetro efectivo D10 igual a 0.3 mm. Estime el coeficiente de permeabilidad.

Solución. La estimación puede hacerse utilizando la ec. 2.4. Así, 

2.- En una prueba de permeabilidad con permeámetro de carga constante se utilizó una muestra de 8 cm de longitud, con diámetro de 5 cm. Tras establecerse el flujo bajo una carga de 50 cm3, se recolectó una descarga de 120 cm en 30 seg. Calcule el valor de k.

Solución. De acuerdo con la ec. 2.5, 

3.- Se realizó una prueba de permeabilidad con un permeámetro de carga variable con diámetro interior de 5 cm. El diámetro interior del tubo vertical fue de 2 mm. La muestra tuvo una longitud de 8 cm. Durante un período de 6 mm, la carga sobre la muestra disminuyó de 100 a 50 cm. Calcule el valor de k.

Solución. De acuerdo con la ec. 2.6,

Prueba de Bombeo de Campo - Suelos.

La información más fidedigna con respecto a permeabilidad de un deposito de material grueso situado abajo del nivel freático, puede obtenerse usualmente haciendo pruebas de bombeo en el campo. Aunque estas pruebas tienen su mayor aplicación en relación con las cimentaciones para presas, también pueden resultar oportunas en los trabajos de cimentación de puentes o edificios grandes, en los que puede hacerse descender el nivel del agua freática. Se hace una prueba perforando un pozo del cual se bombea y varios otros en los cuales se observe la posición del nivel del agua. Los pozos de observación se perforan a varias distancias del pozo de bombeo, siguiendo dos líneas rectas, una orientada aproximadamente en la dirección de la corriente natural del agua subterránea y la otra en ángulo recto a la primera. Una vez que se ha establecido el flujo, y los niveles del agua en todos los pozos son casi estacionarios, puede calcularse el coeficiente de permeabilidad con los resultados de las observaciones. Las ecuaciones pertinentes dependen de las condiciones de frontera y, en algunos problemas prácticos, pueden ser bastante complicadas. Para las condiciones sencillas que se ilustran en la fig. 2.3, que representan un manto horizontal de arena homogénea que se extiende de la superficie del terreno hasta un estrato impermeable, mismo que es atravesado en todo su espesor por el pozo de bombeo y por los pozos de observación,



en la que q es igual al gasto que atraviesa la frontera de cualquier sección cilíndrica que tenga un radio r y, por lo tanto, la cantidad de agua bombeada del pozo por unidad de tiempo.

Tabla 2.1 Coeficiente de permeabilidad de los diferentes suelos. 

Figura 2.3. Ilustración del flujo del agua hacia un pozo durante una prueba de bombeo.

En la tabla 2.1 se han reunido valores aproximados del coeficiente de permeabilidad para diferentes tipos de suelos, y el método recomendado para determinar estos valores. Como se indica en la tabla, es difícil obtener valores seguros para los coeficientes de permeabilidad de los suelos que contengan cantidades apreciables de limo o de arena muy fina. No existe un método indirecto para calcular la permeabilidad de esos materiales, y las pruebas de laboratorio es probable que sean extremadamente inseguras, a menos que las realicen técnicos experimentados.