Sistema de Clasificación de Suelos.

Introducción. Como los depósitos de suelos son infinitamente variados, no ha sido posible crear un sistema universal de clasificación de suelos para diferenciarlos en grupos y subgrupos sobre La base de todas sus propiedades índice importantes. Sin embargo, se han ideado sistemas útiles basados en una o dos propiedades características. Algunos de estos sistemas han llegado a generalizarse tanto entre los trabajadores de los diversos campos en los que intervienen los suelos, que es necesario que el ingeniero posea al menos un conocimiento general de los mismos. Al mismo tiempo, es indispensable tener presente que ningún sistema describe adecuadamente ningún suelo para todos los objetos que persigue la ingeniería. En realidad, muchos sistemas ignoran las propiedades más importantes desde el punto de vista del ingeniero especialista en cimentaciones.

-Sistemas de Clasificación de Suelos Basados en la Textura.

-Sistema de Clasificación de Suelos AASHO.

-Sistema de Clasificación de Suelos Unificado.

-Inconvenientes de las Clasificaciones Ingenieriles.

Limites de Atterberg: Indice de Plasticidad, Liquidez.

Si el contenido de agua de una suspensión espesa de arcilla se reduce gradualmente, la mezcla de arcilla y agua pasa del estado líquido al estado plástico y, finalmente, al estado sólido.

Se ha encontrado que los contenidos de agua correspondientes a las transiciones de un estado a otro, usualmente son diferentes en las arcillas que tienen propiedades físicas diferentes cuando se han remoldeado, y son aproximadamente iguales en las arcillas que tienen propiedades físicas semejantes. Por lo tanto, las fronteras entre los estados de consistencia, pueden servir como propiedades índice, útiles en la clasificación de las arcillas.

El significado de los contenidos de agua que sirven de límite para cada estado físico fue sugerido por primera vez por A. Atterberg en 1911. Por lo tanto, estos límites se conocen comúnmente como límites de Atterberg, y las pruebas para determinarlos se llaman determinación de los límites de Atterberg. En la realidad, al pasar la mezcla de suelo y agua de un estado a otro, no se produce un cambio brusco en las propiedades físicas. Por lo tanto, las pruebas de los límites, son pruebas empíricas, que se

han adoptado para definir los valores de los mismos.

Arriba del límite líquido WL, el sistema de suelo y agua es una suspensión. Abajo del límite líquido y arriba del límite plástico Wp, el sistema de suelo y agua se dice que está en estado plástico. En este estado) el suelo puede deformarse o remoldearse sin la formación de grietas y sin que cambie de volumen. La amplitud de variación de la humedad en la cual el sistema se comporta como material plástico se llama frecuentemente intervalo plástico, y a la diferencia numérica entre el límite liquido y el limite plástico se le llama índice de plasticidad Ip (que con frecuencia se designa PI);

Indice de plasticidad,   Ip =WL - Wp 1.12

Algo abajo del límite plástico, el sistema de agua y suelo llega al límite de contracción ws. La reducción de la humedad del suelo por secado abajo del límite de contracción no se acompaña de disminución de volumen; por el contrario, el aire entra en los huecos del sistema y el material se convierte en no saturado.

Los límites de Atterberg varían con la proporción de arcilla en el suelo, con el tipo de mineral arcilloso, y con la naturaleza de los iones adsorbidos en la superficie de la arcilla. Ya se dijo que las diferencias en la estructura atómica de los minerales arcillosos producen diferencias en las cargas eléctricas que están en las superficies de la arcilla. La existencia de estas cargas la indica la capacidad de las arcillas para adsorber iones de la solución. Los cationes (iones positivos) son más fácilmente adsorbidos que los aniones (iones negativos); por lo tanto) las cargas negativas deben predominar en las superficies de la arcilla. Un catión, como Na+, es fácilmente atraído a la superficie de la arcilla. Sin embargo, el ion adsorbido de Na+ no se une permanentemente; y pueden reemplazarlo iones de K+, Si la arcilla se coloca en una solución de cloruro de potasio KCI. Al  proceso por el que se reemplaza el catión en exceso se le llama intercambio catiónico.

La capacidad de cambio de cationes de los diferentes tipos de minerales arcillosos, puede medirse lavando una muestra de cada uno de ellos en una solución de una sal que comúnmente no se encuentre en estado natural, como el cloruro de amonio NH4C1, y determinando la cantidad adsorbida de NH4+, midiendo la diferencia entre la concentración original y final de la solución de lavado. Conviene expresar la capacidad de intercambio catiónico en función del número de pesos equivalentes de un ion adsorbido por 100 g de mineral arcilloso, ya que este factor es independiente del peso de cada ion adsorbido y del número de cargas que se le asocian.

En la tabla 1.6 se dan los intervalos típicos de capacidades de intercambio cationico de varios minerales arcillosos.

TABLA 1.6 Capacidad de Intercambio Catiónico de los Minerales de la Arcilla

La tabla 1.6 indica que las montmorillonitas son aproximadamente 10 veces más activas para adsorber Cationes que las caolinitas. Por lo tanto, se requiere una cantidad mucho menor de montmorillonita que de caolinita para impartir las propiedades típicas de una arcilla a un suelo que tenga granos mezclados.

Aunque la facultad de adsorber agua en la superficie de un mineral arcilloso varía en el mismo orden que su capacidad de intercambio, también la afecta el tipo de cationes presentes. Por lo tanto, hay ciertas correlaciones entre las propiedades del sistema suelo—agua, tales como los límites de Atterberg, el tipo de mineral arcilloso, y la naturaleza de los iones adsorbidos. La tabla 1.7 presenta el límite líquido y el índice de plasticidad de diferentes minerales de arcilla con distintos iones adsorbidos. Comparando las tablas 1.6 y 1.7 se ve que existe realmente una correspondencia entre la capacidad de intercambio catiónico de una arcilla y sus propiedades con respecto a su humedad, medida por los límites de Atterberg. Resulta también evidente que cuanto mayor es la capacidad de intercambio de cationes de una arcilla, mayor será el efecto al intercambiar el catión adsorbido.

El tipo de mineral arcilloso y la naturaleza de los iones adsorbidos son importantes para la estabilización química de los suelos, en la extracción del agua por métodos eléctricos, y en otros problemas relativamente especializados. Puede obtenerse la información necesaria valiéndose de técnicas como las del análisis por medio de los rayos X. Sin embargo, para la mayor parte de los problemas sobre cimentaciones, la influencia de las características mineralógicas y químicas se acusan en forma adecuada en los valores de los límites de Atterberg.

El límite líquido y el índice de plasticidad constituyen unidos una medida de la 

Tabla 1.7 Valores de los Limites de Atterberg de los Minerales de la Arcilla con Varios Cationes Adsorbidos 

 

plasticidad de un suelo. Los suelos que poseen wL e Ip de grandes valores se dice que son muy plásticos. A los que tienen bajos valores se les llama ligeramente plásticos. La interpretación de las pruebas de los límites líquido y plástico se facilita usando la Carta de plasticidad desarrollada por A. Casagrande. En esta Carta (fig. 1.10), las ordenadas representan valores del índice de plasticidad, y las abscisas, valores del límite líquido. La Carta se divide en seis regiones por la línea inclinada A que tiene por ecuación Ip = 0.73 (WL - 20), y las dos líneas verticales WL = 30 y WL = 50. Todos los suelos representados por puntos arriba de la línea A son arcillas inorgánicas; la plasticidad varía de baja (WL < 30) a alta (WL > 50) con valores crecientes del límite líquido. Los suelos representados por puntos que quedan abajo de la línea A pueden ser limos inorgánicos, limos orgánicos, o arcillas orgánicas. Si son inorgánicos, se dice que son de compresibilidad baja, media o elevada, lo que depende de que su límite líquido sea inferior a 30, esté comprendido entre 30 y 50, o sea superior a 50. Si son limos orgánicos, están representados por puntos situados en la región correspondiente a un límite líquido entre 30 y 50 y, si son arcillas orgánicas, a un límite líquido superior a 50.

La diferencia entre suelos orgánicos e inorgánicos puede hacerse usualmente, ejecutando dos pruebas para determinar dos límites líquidos con el mismo material, 

Figura 1.10. Carta de plasticidad (según A. Casagrande. 14). 

una con suelo húmedo o secado al aire, y otra con el suelo secado en el horno. El secado en el horno produce cambios irreversibles en los componentes orgánicos que producen un límite líquido significativamente inferior. Si el límite de la muestra secada en el horno es inferior a aproximadamente 0.75 veces el de la muestra que no se secó de esa manera, el suelo puede clasificarse como orgánico. Unos cuantos minerales inorgánicos de arcilla y otros componentes de los suelos finos también experimentan cambios irreversibles al secarlos en el horno; por lo tanto, la identificación no puede basarse siempre en los resultados de las pruebas de los límites.

La humedad natural de una arcilla es en sí una propiedad índice útil. Sin embargo, tiene un mayor significado la relación de la humedad natural a los límites líquido y plástico. Los depósitos que tienen humedades cercanas al límite líquido son usualmente mucho más blandos que los que tienen humedades cercanas al límite plástico, Una de las propiedades características más importantes de los depósitos de arcilla natural es, por lo tanto, el índice de liquidez, definido por la ecuación

Puede verse que IL es negativo en los suelos que tengan humedades menores que el límite plástico. Al aumentar el contenido de agua del límite plástico al límite líquido, el valor de IL aumenta de O a 1.0. Si la humedad natural es mayor que el límite líquido, el índice de liquidez es mayor que 1.0. La consistencia de una arcilla remoldeada puede estimarse cuando se conocen su humedad natural y los valores de sus límites. Las relaciones se ilustran en la fig. 1.11.

Ninguna de las pruebas para determinar los límites de Atterberg es difícil de ejecutar, aunque se requiere cierta experiencia para desarrollar la técnica necesaria para obtener resultados reproducibles. La determinación del límite líquido se hace comúnmente, utilizando un aparato mecánico diseñado por A. Casagrande (fig. 1.12). Se coloca una muestra del suelo remoldeado en la copa, y se hace una ranura de 2 mm 

Figura 1.11. Escala de contenidos de agua de un sucio, mostrando los Limites de Atterbert, el estado físico correspondiente, y la consistencia aproximada del suelo rermoldeado.

de ancho en su base, y de 8 mm de altura, en el centro de la pasta de suelo. Luego, el operador da vuelta a la manivela que levanta la copa a cierta altura de manera que el punto de contacto entre la copa y la base quede a un centímetro sobre la base, Desde esta posición la copa cae libremente. El suelo está en el límite liquido, si se requieren 25 golpes para hacer que los extremos inferiores de la ranura queden en contacto entre sí en una longitud de 13 mm. La humedad que tenga la muestra cuando se le da este número de golpes es el límite líquido.

La determinación del límite plástico se ejecuta formando cilindros delgados con una muestra de suelo plástico con un diametro de 3 mm. Si el suelo no se desmorona, se recoge el cilindro, se vuelve a amasar y se rola de nuevo. Se repite este proceso hasta que el cilindro se comienza a desmoronar precisamente cuando adquiera el diámetro de 3 mm. A la humedad a la que se desmorone el cilindro se la define como límite plástico.

El límite de contracción de un suelo se determina preparando una muestra de volumen conocido con una humedad superior al límite líquido, misma que se seca en un horno. Se miden el peso y el volumen de la muestra secada en el horno. Con estos datos y el contenido de agua inicial, se hace un cálculo de la humedad a la que la muestra seca estaría precisamente saturada. Se considera que esta humedad es el límite de contracción.

En los métodos estándar de la ASTM D423, D-424, y D-427, se dan los procedimientos detallados para realizar las pruebas del Límite Liquido, el Limite Plástico y el Límite de Contracción.  

 

Figura 1.12. a) y b) Aparato mecánico para determinar el límite Líquido. c) Ranurador de Casa Grande  d) Ranurador estándar de la ASTM.

Consistencia y Sensibilidad - Suelos.

Indudablemente, la propiedad índice más importante de los materiales finos en estado natural es la consistencia. 

La consistencia de los depósitos naturales de suelos cohesivos se expresa cualitativamente con términos como blando, medio, firme y duro. Sin embargo, el significado de estos términos varía mucho en las diferentes partes del país, lo que depende de que los suelos locales sean generalmente duros o generalmente blandos. En vez de fiarse de términos tan vagos, el ingeniero debe adquirir la facultad de estimar la resistencia a la compresión del suelo.

Cuantitativamente, la consistencia de un suelo cohesivo inalterado puede expresarse en función de su resistencia a la compresión qu. (determinada en probetas sin confinar). 

En la prueba que se hace para determinar esta resistencia se utiliza un prisma o cilindro de suelo que tenga una altura de 1 1/2 a 2 veces el diámetro medio, que se carga hasta que falle, a la compresión simple, haciendo la prueba con suficiente rapidez para que no cambie la humedad del suelo. El equipo ilustrado en la fig. 1.9 es el que comúnmente se usa en la prueba. Se hacen observaciones simultáneas de la carga y del acortamiento vertical. La carga de falla o, si la muestra no se rompe, la carga necesaria para producir una deformación unitaria de 20 por ciento se expresa como la carga por unidad de área de la sección transversal, en kg por centímetro cuadrado. En la tabla 1.5 se indica la relación entre los términos cualitativos que describen la consistencia y los valores cuantitativos de la resistencia a la compresión simple. Si no se dispone del equipo para hacer pruebas de compresión simple, puede obtenerse una estimación aproximada de dicho valor utilizando las pruebas de campo sencillas que se sugieren en la tabla 1.5.

Cuando se amasa con las manos una muestra de arcilla inalterada sin que se modifique su humedad, generalmente se ablanda. Puede investigarse esta característica, remoldeando sin que pierda agua, una muestra del material que se probó anteriormente a la compresión; introduciendo luego el material amasado en un molde cilíndrico, extrayendo la muestra remoldeada, y haciendo con ella una prueba de compresión simple. 

Figura 1.9. Aparato del tipo comúnmente usado  para determinar la resistencia a la compresión en muestras sin confinar de suelos.

La relación 

se conoce como la sensibilidad de la arcilla. Algunas arcillas con estructuras secundarias que pueden caracterizarse como grietas, juntas, o superficies de resbalamiento, pueden tener sensibilidades menores que 1. La sensibilidad de la mayor parte del resto de las arcillas excede de 1

Tabla 1.5 Expresiones Cualitativas y Cuantitativas de la Consistencia de las Arcillas 

 

pero no pasa de aproximadamente 8. Los suelos naturales en que los valores de la sensibilidad son mayores de 4, se conocen como arcillas sensibles, y si la sensibilidad pasa de 8, se les llama arcillas supersensibles. Hay arcillas de extrema sensibilidad en que este valor sobrepasa 15 (quick clays). Estas arcillas deben tratarse con cuidado durante la construcción, porque con sus operaciones se producen alteraciones que tienden a transformarlas, al menos temporalmente, en liquidos viscosos. Antes de remoldearlas, las arcillas muy sensibles pueden tener una estructura floculada suelta (fig. 1 .8b), mientras que, al remoldearlas puede producirse una estructura dispersa (fig. 1.8c).

Si se deja en reposo una muestra de arcilla remoldeada, sin que sufra más alteraciones y sin que cambie su humedad, puede recuperar cuando menos parte de su resistencia y dureza originales. Este aumento de resistencia se debe a una reorientación gradual de las moléculas de agua adsorbidas, y se conoce como tixotropía.

Estructura y Consistencia de los Suelos - Estructura primaria y secundaria.

 La estructura primaria se refiere a la forma en que están dispuestos los granos en un suelo. Esta disposición se forma usualmente durante el proceso de sedimentación o de meteorización de la roca. Además, pueden producirse varias discontinuidades después de la deposición o formación del suelo, que constituyen la estructura secundaria del depósito. Corresponden a fenómenos como la formación de sistemas de juntas en las rocas sedimentarias.

La estructura primaria puede describirse como simple, floculada, o dis persa. En la estructura simple (fig. 1.8a), cada grano toca a varios de sus vecinos, de manera que el conjunto es estable aunque no hubiera fuerzas de adherencia en los puntos de contacto entre granos. El acomodo puede ser compacto o suelto, y las propiedades del conjunto resultan muy afectadas por la compacidad.

En las figs. 1.8b y 1.8c se representan conceptos sobre la estructura de los suelos finos. Las partículas de forma oval re presentan granos de limo, mientras que las partículas de lados planos representan láminas de minera! arcilloso. En la estructura floculada (fig. l.8b), el borde o esquína de una laminilla de arcilla tiende a ser atraída a la cara plana de otra. En consecuencia, las partículas presentan una estructura suelta pero bastante estable que puede mantenerse mientras las cargas eléctricas en los bordes de las placas conserven

Figura 1.8. Diagrama que i1usra a) estructura simple densa b) estructura floculada y c) estructura dispersa. 

un signo opuesto a las de las caras. El grado de holgura de esta disposición depende, cuando menos en parte, de la naturaleza y cantidad de electrólitos presentes durante la sedimentación. En la estructura dispersa (fig. 1.8c), los bordes, esquinas, y caras de las láminas de arcilla tienen cargas eléctricas semejantes. Así, las partículas se repelen entre sí y toman posiciones casi paralelas. Aunque la estructura dispersa pudiera haber estado muy suelta cuando se efectuó la sedimentación, la presión puede obligar a las plaquitas adyacentes a llegar a un estado más denso más fácilmente que si poseyeran la estructura floculada de la fig. l.8b.

Los tipos principales de estructura secundaria los forman las grietas, juntas, superficies de resbalamiento, y concreciones. Las grietas y juntas se forman comúnmente como resultado de la desecación, algunas veces después de la de- posición del material. Las superficies de resbalamiento son superficies pulidas en las arcillas duras que han experimentado movimiento diferencial o expansión. Las concreciones son acumulaciones de carbonatos o de compuestos de hierro, Todos estos detalles rompen la continuidad de la masa de suelo y pueden impartirle propiedades muy diferentes a las de las muestras tomadas del depósito que no contengan estas discontinuidades.

Suelos: hallar el peso volumétrico del suelo seco, peso volumétrico del suelo saturado.

Una muestra de suelo compactada de acuerdo con la prueba Proctor Estándar tiene un peso volumétrico de 2100 kg/m3 a 100 por ciento de compactación y una humedad óptima de 14.0 por ciento. ¿Cuál es el peso volumétrico del suelo seco? ¿Cuál es el peso volumétrico cuando el aire en los huecos es cero? Si los huecos se llenan de agua, ¿cuál sería el peso volumétrico del suelo saturado? Supóngase que la materia sólida tiene un peso especifico de 2.67. 

Solución. Puede representarse el problema con el croquis que se acompaña, suponiendo que el volumen es 1 m3.

Como la humedad es de 14 por ciento, podemos escribir, por definición:

Entonces, el volumen de vacíos es 1.00 -  0.69 = 0.31 m3.
El volumen de agua es 258/1000 =  0.26 m3.
Entonces el volumen de aire es 0.31 - 0.26 =  0.05m3.

Si se expulsara de la muestra todo el aire, el peso volumétrico seco con cero huecos sería, por definición,

Por otra parte, si los huecos estuvieran llenos de agua, el peso del agua sería:

    0.31 X 1,000= 310kg 

y el peso volumétrico del material saturado seria: 

Calcular el grado de saturación y la Compacidad Relativa de una Muetra de Arena.

Se encontró que una muestra de arena situada arriba del nivel del agua freática tenía una humedad natural de 15 por ciento y un peso volumétrico de 1922 kg/m3.

Las pruebas de laboratorio efectuadas en una muestra seca, indicaron valores para
emin = 0.50 y para emáx = 0.85 cuando estaba más suelta y más compacta, respectivamente. Calcule el grado de saturación y la Compacidad Relativa. Supóngase que G = 2.65.

Solución.  En este problema, por comodidad, puede tomarse el volumen total de un m3, siendo por tanto el peso total  1922 kg. Este es también el peso del suelo más el agua. Estos valores pueden escribirse en un croquis, como se muestra.

Como la humedad es de 15 por ciento, podemos escribir, por definición: 

Estos valores pueden ahora escribirse al lado derecho del diagrama.

El volumen de sólidos es: 

Por diferencia, el volumen de aire es 1.0 -  (0.63 + 0.25) = 0.12 m3. El volumen de huecos es, por tanto, 0.37 m3.

Por definición, el grado de saturación es:

 

Relación de Vacíos, la Porosidad y el Peso Volumétrico Saturado de una Muestra de Arcilla Blanda.

Una muestra de arcilla blanda, saturada, tiene un contenido de agua natural de 43 por ciento. El peso específico relativo de sus sólidos es 2.70.

¿Cuáles son la relación de vacíos, la porosidad y el peso volumétrico saturado?

Solución. Puesto que el suelo está completamente saturado, el croquis que se anexa representa las relaciones gravimétrica y volumétricas del caso. Como se conoce la humedad, las cantidades que están al lado derecho del diagrama pueden fijarse inmediatamente, en el supuesto de que Ws = 1.0 g.

Después se calcula el volumen de sólidos y se registra al lado izquierdo. Es igual a 1.00/2.70 = 0.37 cm3. Ya que el peso especifico del agua es igual a la unidad, puede registrarse el volumen del agua como
0.43 cm3. Por lo tanto, puede tomarse el volumen total como 0.43 + 0.37 = 0.80 cm3. Entonces, por definición, 

Relaciones Volumétricas y Gravimétricas de los Suelos.

Definiciones. Lo suelto o lo compacto de una muestra de suelo puede determinarse cuantitativamente en el laboratorio. Los términos porosidad, relación de vados, y el peso especifico relativo de los sólidos se usan comúnmente para definir la densidad de la muestra. La fig. 1.4 es un diagrama de una muestra de suelo en un recipiente sellado, con el aspecto que presentaría si fuera posible separar las fases sólida, líquida y

gaseosa. El volumen de sólidos se designa por el símbolo Vs, el volumen de agua por y el volumen de gas por V10. Como la relación entre V9 y V10 cambia usualmente con las condiciones del agua en el subsuelo, así como bajo el efecto de las cargas aplicadas, es conveniente designar todo el volumen que no está ocupado por material sólido como volumen de vacíos, Vv,. Si se designa el volumen total de la muestra por V, entonces la porosidad se define con la ecuación: 

Usualmente, este valor se expresa como porcentaje. Cuando un suelo se comprime, cambian los valores de la ecuación anterior tanto del numerador como del denomi-

Figura 1.4. Diagrama de una muestra de suelo que ilustra el significado de los símbolos usados en relaciones gravimétricas y volumétricas. 

nador, por lo que es conveniente en muchos de los cálculos que es necesario efectuar para determinar los asentamientos, referir el espacio vacío a un denominador invariable. Por esta razón se usa la cantidad conocida como relación de vacíos u oquedad. Se define como:

Una de las propiedades índice más importantes de los suelos finos es el contenido de agua o humedad, w. Se define como: 

En esta ecuación, Ww es el peso del agua y Ws, es el peso de la materia sólida secada en el horno. El peso del agua se refiere a la cantidad invariable Ws. en vez de al peso total de la muestra. Al aumentar la temperatura de una mezcla de suelo y agua que se está secando, la mezcla continúa perdiendo humedad, hasta que a una temperatura relativamente elevada, los minerales que constituyen el suelo se descomponen y pierden el agua de constitución. Por esta razón, las comparaciones de humedades no tienen significado, a menos que la temperatura a la que se seca el suelo se estandarice. La temperatura estándar del horno es de 105° a 115°C. 

Muchos suelos que se encuentran abajo del nivel del agua freática y algunos suelos finos que están arriba del mismo, se encuentran saturados. Sin embargo, los vacíos de la mayor parte de los suelos que están arriba del nivel del agua freática están

llenos en parte de agua y en parte de aire. Incluso algunos suelos sumergidos tienen una proporción importante de aire o de gas. El grado de saturación se define como:

Grado de saturación,

Por lo tanto, cuando el grado de saturación es de 100 por ciento todo el espacio vacío está lleno de agua.

El peso por unidad de volumen o peso volumétrico ‘y es una de las propiedades físicas más importantes de un suelo. Por ejemplo, deberá conocerse para poder calcular la presión de tierra o la producida por sobrecargas.

Por definición: 

en la que W es el peso total del suelo incluyendo el agua y V es el volumen total. Es conveniente indicar los valores especiales del peso volumétrico por medio de subíndices. Si el suelo está completamente saturado, es decir, si Vg = O, su peso volumétrico se designa por γsat  Si el suelo está secado en el horno, su peso se indica con γd , llamándose peso volumétrico seco, y se define. 

Si se conoce la humedad, puede calcularse el peso volumétrico seco de la siguiente manera: 

En estudios de compactación de suelos en ocasiones es útil calcular el peso volumétrico seco que se hubiera obtenido, si se hubiera disminuido el volumen de una muestra húmeda, expulsando el aire hasta que el grado de saturación de la muestra llegara al 100 por ciento. A este estado se le designa exento de huecos con aíre. 

Este peso volumétrico puede calcularse con la expresión: El peso volumétrico del suelo seco exento de huecos con aire, 

En la práctica, con frecuencia es inconveniente determinar directamente el valor de γ, midiendo el peso total y el volumen total. Es más común determinarlo indirectamente basándose en el conocimiento del peso volumétrico de los componentes sólidos γs. Esta cantidad se define como:
Peso unitario de los componentes sólidos, 

Frecuentemente, es preferible utilizar el peso específico relativo de los sólidos G, definidos como:
Peso específico relativo de los sólidos G, 

Definidos como:

Peso especifico relativo de los solidos.

donde γw es el peso volumétrico del agua, tomado como 1 g/cm3. El valor de γs, o G puede determinarse por pruebas en el laboratorio, pero puede estimarse usualmente con suficiente precisión. Para los cálculos de rutina, puede tomarse como 2.65 el valor de G para las arenas. Las pruebas efectuadas en gran número de suelos de arcilla han indicado que el valor de G usualmente está comprendido en el intervalo de 2.5 a 2.9 con un valor promedio de aproximadamente 2.7.

La tabla 1.3 proporciona el peso específico relativo de los sólidos de los componentes de los suelos más importantes. Puede ayudar a estimar el valor de G para un suelo de composición mineralógica conocida.

En la tabla 1.4 se da una lista de los valores típicos de la porosidad, relación de vacíos, y de pesos volumétricos de varios suelos.

Densidad del agregado del suelo. En el comportamiento del suelo influye mucho lo suelto o lo compacto de su estructura. Sin embargo, es necesario señalar una diferencia a este respecto entre los suelos de grano grueso sin cohesión y los materiales cohesivos. En una masa de suelo de grano grueso, la mayor parte de los granos tocan a otros, produciendo contactos de punto a punto, y los esfuerzos que se hagan para compactar la masa pueden reducir la relación de vacíos solamente por el reacomodo de las partículas o por su ruptura. Por otra parte, la densificación de los suelos finos, especialmente de la arcilla, depende de otros factores como la cohesión y la presencia de películas de agua sobre las superficies de las partículas.

Tabla 1.3 Peso Específico relativo de los más Importantes Componentes del Suelo 

Tabla 1.4  Porosidad, Relación de vacíos, y Peso volumétrico de Suelos Típicos en Estado Natural.

La relación de vacíos o la porosidad de cualquier suelo usualmente no proporcionan de por sí una indicación directa de su comportamiento cuando se carga o cuando se excava. De dos suelos gruesos que tengan la misma relación de vacíos, uno puede estar muy compacto mientras que el otro puede estar suelto. Por lo tanto, la compacidad relativa de un material grueso es más importante que la sola relación de vacíos. La compacidad puede expresarse numéricamente por la Compacidad Relativa Id, que se define como: 

en la que emax, es la relación de vacíos del suelo en su estado más suelto; e es la relación de vacíos real; y emin  es la relación de vacíos en el estado más compacto posible. Por tanto, Id = 1.0 para los suelos muy compactos, y O para los suelos muy sueltos.

En la práctica, la Compacidad Relativa de los suelos granulares usualmente se juzga de manera indirecta mediante pruebas de penetración o de carga , porque la medida directa de la relación de vacíos en el campo no resulta práctica. Sin embargo, si se conoce e, pueden determinarse los valores de tm Y tmjn en el laboratorio. El estado más suelto generalmente puede obtenerse permitiendo que el material pulverizado y seco caiga en un recipiente desde un embudo sostenido de manera que la caída libre sea aproximadamente de 1.3 cm. Si el material es limoso, puede lograrse que quede más suelto permitiéndole que se asiente en agua. El estado más denso generalmente puede obtenerse apretando el suelo dentro de un recipiente por medio de una combinación de presión estática y vibración o, en algunas ocasiones, “haciendo llover” la arena desde una altura que permita que el impacto de los granos al caer compacte la capa superficial.

Los procedimientos estándar de la A STM describen varios medios de producir el Ya que distintos procedimientos conducen a diferentes relaciones de vacíos en los diversos materiales, los valores numéricos de emáx y de emin , no siempre pueden determinarse definitivamente. En consecuencia, el valor de Id queda algo indeterminado y debe acompañarse de descripciones de la manera que se empleó, para determinar emáx y emin.

En los suelos que contienen cantidades apreciables de limo o arcilla, la Compacidad Relativa pierde su significado, porque los valores de e míx y de e mm no tienen sentido definido. En muchas operaciones de construcción intervienen estos materiales. Además, los efectos benéficos que resultan al compactar estos suelos han sido demostrados por una larga experiencia. La necesidad de un método para definir el grado de compactación condujo, a principios de la década de los treintas, a la elaboración en California de un método de prueba para la compactación en el laboratorio (Proctor, 1933). Esta prueba ha sido perfeccionada y estandarizada por la ASTM y la AASHO como prueba para determinar las relaciones entre el contenido de agua y el peso volumétrico seco (ASTM título D-698 o método AASHO T-99). El aparato comúnmente usado se ilustra en la fig. 1.5. Consta de un cilindro metálico que tiene un volumen de 944 cm y un diámetro interior de 10.2 cm, en combinación con un pisón metálico con un peso de 2.495 kg y una cara circular de 5.1 cm de diámetro. El suelo se coloca en el cilindro en tres capas aproximadamente iguales. Cada capa se compacta con 25 golpes de pisón dejándolo caer libremente desde una altura de 30.5 cm. (En una alternativa del procedimiento se permite el uso de un molde que tiene un diámetro de 15.2 cm con un volumen de 2124 cm3 se aplicari 56 golpes del martillo estándar a cada una de las tres capas.) Después de la compactación, el suelo se enrasa respecto a la parte superior del cilindro y se determina el peso del suelo contenido en el recipiente. Luego se extrae una muestra de enmedio del cilindro compactado de suelo para determinar la humedad.

Con el peso y el volumen del suelo del recipiente, se calcula el peso volumétrico γ del suelo. Sin embargo, la medida de la compactación, es el peso volumétrico seco γd, es decir, el peso por metro cúbico de los componentes sólidos del suelo que están en el recipiente. Los valores de 7d se determinan para una serie de muestras de suelo, cada una de las cuales tiene una humedad inicial diferente. Ordinariamente, las primeras determinaciones se hacen 

Figura 1.5.  Equipo usado para determinar las curvas de compactación relaciones de la humedad de los suelos (Métodos ASRM D-698, AASHO T-99)

con el suelo bastante seco; las determinaciones sucesivas se hacen con suelos progresivamente más húmedos, hasta que el peso del suelo húmedo que puede introducirse en el molde alcanza un máximo y comienza a decrecer.

El procedimiento que se acaba de describir se conoce en muchos lugares con el nombre de Prueba Proctor Estándar, fue ideado para duplicar en el laboratorio, con la mayor aproximación posible, los resultados que podían obtenerse con el equipo usado comúnmente en la década de los treintas para la compactación de suelos en el campo. Desde entonces, el equipo de compactación en el campo se ha perfeccionado al punto que es posible obtener pesos volumétricos secos mayores que por el procedimiento Proctor Estándar. Las mayores compactaciones se requieren frecuentemente en la construcción de aeropistas y presas altas. Por esta razón, se han usado otras normas de compactación, en conexión con esfuerzos de compactación mayores. Al más común de estos, se le llama a veces prueba AASHO Modificada, pero más correctamente se le designa como método ASTM D-1557 o método AASHO T-180, y también puede hacerse con el molde mostrado en la fig. 1.5. La cara del pisón tiene las mismas dimensiones, pero su peso se ha aumentado a 4.53 kg y la altura de caída a 45.7 cm. Además, el suelo se compacta con 25 golpes en cada una de cinco capas, en lugar de tres. (Puede usarse como alternativa el molde de 15,2 cm; el número de golpes por capa se aumenta entonces a 56.)

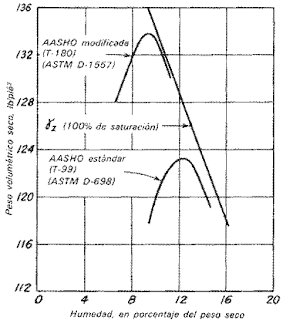
Los resultados se representan con curvas de compactación en las que la γd para cada determinación, se dibuja contra el valor correspondiente de la humedad de moldeo w. La ordenada del máximo de la curva se designa como peso volumétrico máximo seco γmáx, O 100 por ciento de comactación, y la abscisa se llama humedad óptima wopt. La fig. 1.6 muestra las curvas de compactación obtenidas en una morrena glacial, empleando los dos métodos de compactación. También aparece la relación entre el peso volumétrico seco γz sin huecos llenos de aire y la humedad de compactación w. Como la línea que representa

Figura 1 .6. Curvas de compactación para una morrena glacial, usando dos energías de compactación diferentes.

esta relación corresponde a una saturación de 100 por ciento, debe quedar a la derecha de todos los puntos de cualquier curva de compactación.

Los dos procedimientos de la ASTM para ejecutar las pruebas de compactación conducen, como se ilustra en la fig. 1.6, a dos diferentes relaciones de humedad-peso volumétrico seco para el mismo suelo. De manera similar, se obtendrían en el campo curvas diferentes, dependiendo del tipo, peso, y número de pasadas del equipo de compactación o de los espesores de las capas que se compactan. Por lo tanto, términos como humedad óptima, o compactación de LOO por ciento, no representan propiedades únicas de un suelo especial, sino que dependen también del procedimiento de compactación. Por esta razón, debe definirse siempre el procedimiento cuando se dan valores de wopt o de γmax.

Sin embargo, el tipo de suelo es la variable principal para establecer las relaciones de la humedad al peso volumétrico seco. La influencia en los resultados de las pruebas ejecutadas en los diferentes suelos, de acuerdo con el método D-698 de la ASTM, se ilustra en la fig. 1.7. Es evidente que no solamente cambian las formas de las curvas al variar la textura de los suelos de  gruesa a fina, sino que también cambian las posiciones de las curvas.

Figura 1.7. Curvas de comparación para varios tipos de suelos determinadas por el método de la ASTM D - 698.

Como uno de los objetivos principales de las pruebas de compactación es controlar la compactación del suelo en el campo, siempre deben efectuarse pruebas del suelo compactado en el campo, para comprobar si se ha alcanzado el peso volumétrico deseado. Las especificaciones para construir terraplenes compactados varían según el tipo de cargas a las que va a estar sujeto el suelo. Comúnmente, las especificaciones requieren que los pesos volumétricos secos que se obtengan, posean cuando menos el 95 por ciento del peso volumétrico seco determinado, tomando como base el método D-698 de la ASTM.

Mismo que pudiera llamarse 95 por ciento de la compactación Estándar AASHO. Las subrasantes de las aeropistas que soportan grandes cargas, usualmente tienen que compactarse a un 98 por ciento de la prueba modificada AASHO (ASTM D-1557). Rara vez pueden satisfacerse estas especificaciones tan rígidas, a menos que la humedad del suelo se

aproxime a la óptima correspondiente. En efecto, estudiando la fig. 1.6 resulta evidente que ningún esfuerzo de compactación aplicado a un suelo puede producir, a una humedad dada, un peso volumétrico seco mayor que el indicado por la línea de  γs. Así, si la morrena glacial tuviera una humedad natural de 16 por ciento, el límite superior de su peso volumétrico seco sería aproximadamente 1890 kg/m3. Para producir un peso volumétrico seco cercano al máximo estándar de la AASHO, el suelo tendría que secarse a aproximadamente 14 por ciento, y para alcanzar un peso volumétrico seco cercano al de la prueba modificada, el secado habría de ser hasta un 10 por ciento.

El peso volumétrico de un suelo compactado en el lugar, se determina con una prueba de campo para ese objeto. Comúnmente, se emplean dos procedimientos. En ambos, primero se nivela la superficie del sucio en que se hace la prueba, y luego se hace un agujero de 7 a 15 cm de diámetro muy cuidadosamente a través de la capa compactada. Los lados del agujero deberán quedar tan lisos como sea posible y todo el suelo excavado debe guardarse cuidadosamente. El suelo húmedo extraído debe pesarse cuidadosamente, antes de que pueda evaporarse cualquier cantidad de agua y se toma una muestra relativamente grande para determinar la humedad. Luego se determina el volumen del agujero (1), llenándolo con arena seca, uniforme, que fue calibrada utilizando un cono es pedal para la arena que es el dispositivo (ASTM D-1556, AASHO T-147), o (2) introduciendo un globo de hule lleno de agua de un recipiente calibrado, leyendo el volumen directamente (ASTM 0-2167). Con el método en que se emplea el cono para la arena, el volumen del agujero se determina de la diferencia en peso del recipiente y el cono para la arena, antes y después de llenar el agujero, conociendo el peso volumétrico que toma la arena cuando cae libremente del recipiente. Por lo tanto, en el lugar de la prueba es necesario tener una balanza y arena seca y limpia suficiente. El peso volumétrico del suelo en el lugar se calcula dividiendo el peso del suelo extraído por el volumen del agujero, y

se convierte al peso volumétrico seco por medio de la ec. 1 La. Entonces, el grado de compactación se define como una relación, multiplicada por 100, del peso volumétrico máximo seco γmax en el lugar, entre el mismo, pero determinado en el laboratorio. Se hace resaltar que, a diferencia de la definición de la Compacidad Relativa, la definición del grado de compactación es arbitraria en cuanto a que depende de los detalles del procedimiento de prueba. Además, la resistencia de un suelo dado, ya sea durante o después de la compactación, no está relacionada en forma sencilla al grado de compactación.

La humedad de campo y el peso volumétrico también pueden determinarse con aparatos nucleares colocados sobre una superficie plana de suelo compactado. Estos instrumentos tienen una gran ventaja con relación a los métodos convencionales, que es el poco tiempo que se necesita para hacer una prueba. Hasta ahora, estos instrumentos son muy costosos y con frecuencia están plagados de errores debidos a la mala calibración o por ajustes incorrectos. A pesar de estas desventajas, el uso de los medidores nucleares está aumentando rápidamente porque permiten hacer más pruebas en un tiempo dado, lográndose de esta manera, un control más rápido de la compactación de campo.

Relaciones entre las propiedades. Las diferentes propiedades de los suelos estudiadas en este artículo están interrelacionadas y cada una de ellas puede calcularse en función de otras valiéndose de expresiones algebraicas. Sin embargo, generalmente resulta mas expedito resolver los problemas por medio del diagrama de la fig. 1.4, y las ecuaciones que definen las diferentes cantidades. La sencillez de este procedimiento se hará evidente al estudiar los problemas ilustrativos siguientes.

Propiedades de las Partículas Sólidas - Suelos.

Tamaño de los granos. La propiedad más importante de los granos en los suelos de grano grueso es su distribución granulométrica o por tamaños, que se determina por medio de un análisis mecánico, Los tamaños de los elementos en granos gruesos pueden determinarse usando un juego de cribas. La malla que se usa más comúnmente en el campo o en el laboratorio es la no. 200 U. S. estándar, en la que la anchura de las mallas es de 0.075 mm. Por esta razón se ha aceptado como la frontera estándar entre los materiales de grano grueso y los de grano fino.

Para determinar la distribución granulométrica de las partículas de cualquier suelo que contenga material de grano fino, deberá usarse el método de análisis mecánico en húmedo. Los métodos de análisis en húmedo se basan en la ley de Stokes, que dice que la velocidad a la que cae una partícula esférica a través de un medio líquido es función del diámetro y del peso específico de la partícula. Se hace una suspensión del suelo, que se agita y luego se deja en reposo. Después que ha transcurrido un tiempo dado, todas las partículas mayores que las de un tamaño determinado se han asentado abajo de un plano situado a una profundidad arbitraria en la suspensión. Este tamaño puede calcularse por medio de la ley de Stokes, La densidad correspondiente de la suspensión a la profundidad arbitraria es la medida de la cantidad de suelo menor que el tamaño calculado. De esta manera, midiendo la densidad en tiempos diferentes, puede determinarse la distribución de los tamaños de las partículas.

En ingeniería, la densidad se mide usualmente con un hidrómetro. En el método D-422 de la ASTM se establecen los detalles del procedimiento. Se dispersa en un litro de agua destilada una muestra de aproximadamente 50g de suelo y se vierte  en una probeta para sedimentación. Se agita la suspensión aproximadamente durante un minuto y se coloca la probeta en posición vertical sobre una superficie plana horizontal. Se introduce un hidrómetro especial de forma aerodinámica en la suspensión, y se toman lecturas de la densidad en varios intervalos de tiempo. Se acostumbra tomar lecturas a los 2, 4, 8, 15 minutos, y así sucesivamente. Los cálculos que se basan en estas lecturas permiten obtener la distribución granulométrica de las partículas, con la hipótesis de que todas las partículas son esféricas. En la realidad, las partículas de suelo más finas no son esféricas, sino que tienen forma de laminillas o de agujas. Por lo tanto, el tamaño de partículas que se determina es el diámetro de una esfera que se asentaría en la suspensión COn la misma velocidad que la partícula de suelo.

Una de las fuentes de error más comunes que intervienen en el análisis mecánico en húmedo es la inadecuada dispersión de las partículas de suelo de grano fino. El laboratorista puede creer que está determinando los tamaños de las partículas separadas, mientras que en realidad puede estar midiendo los tamaños de los flóculos compuestos de varias partículas. Para evitar la floculación, se añade a la suspensión una pequeña cantidad de un electrólito que se conoce con el nombre de agente dispersor. No hay manera de determinar por los medios ordinarios de laboratorio cuando se ha obtenido la dispersión máxima. Por tanto, algunas veces es necesario recurrir a diferentes métodos de dispersión, si hay razones para dudar de la validez de los datos obtenidos. Se ha encontrado que los compuestos polifosfatados son generalmente los agentes de dispersión más efectivos. El más usado comúnmente es el hexametafosfato de sodio, pero en algunas ocasiones el fosfato trisódico puede producir una dispersión más completa.

El uso del microscopio electrónico permite a los investigadores determinar la forma y tamaño real de las partículas de suelo de grano fino, pero este refinamiento no resulta práctico ni económico en la clasificación de rutina de los suelos. 

Los resultados de los análisis mecánicos se presentan usualmente por medio de una curva de distribución granulométrica. El porcentaje P de material más fino que el de un tamaño determinado se dibuja en el eje de ordenadas, a escala natural, y el diámetro correspondiente de la partícula, D, en milímetros, se dibuja en el eje de abscisas, a escala logarítmica. Una gráfica de ese tipo tiene la ventaja que los materiales de igual uniformidad se representan por curvas de forma idéntica, sea el suelo de grano grueso o de grano fino. Además, la forma de la curva es una indicación de la granulometría. Los suelos uniformes están representados por líneas casi verticales, y los suelos bien graduados por curvas de forma de S que se extiende a través de varios ciclos de escala logarítmica. La fig. 1.2 muestra curvas de los tamaños de las partículas para suelos de varios tipos.

Las características granulométricas de los suelos pueden compararse más cómodamente, estudiando ciertos valores numéricos importantes deducidos de las curvas de distribución. Los dos más comúnmente usados por los ingenieros se designan como D10, el diámetro efectivo, y Cu =  D60/D10, el coeficiente de uniformidad. El diámetro efectivo es el diámetro de la partícula correspondiente a P = 10 por ciento en la curva granulométrica. Por lo tanto, el 10 por ciento de las partículas son menores que el diámetro efectivo y el 90 por ciento, son mayores (vea la fig. 1.2). Es posible tener un suelo de granulometría discontinua con un coeficiente de uniformidad grande que esté realmente compuesto de dos fracciones uniformes. El coeficiente de curvatura,

,es un valor que puede usarse para identificar esos suelos como mal graduados. En las gravas bien graduadas Cu es mayor que 4 y Cz queda entre 1 y 3 En las arenas bien graduadas, Cu es mayor que 6 y Cz. está entre 1 y 3. (Consulte el título D-2487 de la ASTM, Clasificación de suelos para la ingeniería,)

Composición mineralógica. La propiedad más importante de los granos de los materiales de grano fino de los suelos es la composición mineralógica. Si las partículas del suelo son más pequeñas que 0.002 mm, la influencia de la fuerza de la gravedad en cada partícula es insignificante comparada con las fuerzas eléctricas que actúan en la superficie de la partícula. Un material en el que predomina la influencia de las cargas superficiales se dice que está en estado coloidal. Las partículas coloidales del suelo consisten principalmente en minerales de arcilla, que se originaron de los minerales de las rocas por meteorización, pero que tienen estructuras cristalinas que difieren de los minerales originales.

 FIGURA 1.2  Curvas típicas de distribución granulométrica de alguno suelos naturales. (1) Gravilla, Gastle Tock.colo. (2) Grava de río Denver, Colo. (3) Morrena glacial, Peoria. III.  (4) Arena, Grenada, Miss (5) Polvo de roca glacial, Winchester, Mass (6) Limo arcilloso, Smead. Mont.  (7) Arcilla limosa, Marathon, Ontario , Can.

Los tres grupos más importantes de los minerales de arcilla son la esmect ita, la illita, y la caolinita. Todos ellos son silicatos de aluminio hidratados. Los resultados de los estudios en que se ha utilizado el microscopio electrónico y las técnicas de difracción de los rayos X, demuestran que los minerales de arcilla tienen una estructura reticular, en la que los átomos están dispuestos en varias capas, semejantes a las páginas de un libro. La disposición y la composición química de estas capas determina el tipo de material de arcilla.

Las unidades estructurales básicas de los minerales de arcilla son el tetraedro silícico y el octaedro aluminico. 

Estas unidades se combinan formando capas de tetraedros y de octaedros para producir los diferentes tipos de arcillas. Los minerales de dos capas tienen una sola capa de tetraedros unida a una hoja sencilla de octaedros para formar una estructura reticular de 1:1. La caolinita es un mineral típico de dos capas. En los minerales de tres capas una capa sencilla de octaedros queda entre dos capas de tetraedros para dar una estructura reticular de 2:1. La fig. 1.3 es un croquis de la estructura de la montmorillonita, una de las esmectitas, representativa de la retícula 2:1. La estructura de la illita es semejante, pero algunos de los átomos de silicio han sido reemplazados por aluminio y, además, están presentes iones de potasio entre las hojas tetraédricas de cristales adyacentes.

Las diferencias en la configuración estructural de las retículas de la arcilla, en combinación con las variaciones causadas por la sustitución de otros átomos por el silicio y el aluminio, producen diferencias de intensidad en las cargas eléctricas que existen en las superficies de las diferentes clases de arcillas. Estas a su vez producen diferencias en las propiedades químicas. 

Figura 1.3. Croquis diagrarnatico de la estructura de la rnontmorillonita (según Grim. 1962).

Propiedades Indice de los Suelos.

En el artículo anterior se describieron métodos sencillos para identificar la mayor parte de los componentes de los suelos. Sin embargo, estos métodos representan solamente el primer paso en la descripción adecuada de esos materiales, que debe completarse con otros procedimientos que den resultados cuantitativos que puedan relacionarse a las propiedades físicas que interesan directamente al ingeniero. Las pruebas necesarias para este objeto se conocen como pruebas de clasificación, y los resultados como propiedades índice de los suelos.

Ejecutando las pruebas convenientes de clasificación y determinando las propiedades índice correspondientes, el ingeniero adquiere medios para describir con precisión un suelo dado sin usar descripciones verbales que están sujetas a malinterpretaciones debido a la vaguedad de la terminología. El desarrollo de la facultad de pensar en los suelos en función de valores numéricos de sus propiedades índice, debe ser uno de los objetivos principales de todo ingeniero interesado en cimentaciones.

Las propiedades índices pueden dividirse en dos tipos generales, en propiedades de los granos de los suelos y propiedades del agregado o conjunto. Las propiedades de los granos son las correspondientes a las partículas individuales de que está compuesto el suelo, sin hacer referencia a la manera en que estas partículas están dispuestas en un depósito de suelo. Así, es posible determinar las propiedades de los granos de cualquier muestra de suelo, esté alterada o no. Por otra parte, las propiedades del suelo en conjunto, dependen de la estructura y disposición de las partículas en la masa del suelo. Aunque comúnmente se usan las propiedades de los granos para fines de identificación, el ingeniero debe saber que las propiedades del suelo en conjunto tienen una mayor influencia en el comportamiento desde el punto de vista técnico de un suelo.

Tabla 1.2 Identificación de suelos finos con pruebas manuales

Dimensionamiento de Vigas en Estado II.

La versión 2005 del reglamento CIRSOC 201, basado en la norma ACI 318, indica tratar como viga de gran altura aquellas con luces libres entre apoyos L <= 4h, siendo h la altura total de la viga. Asimismo los casos de vigas con cargas concentradas ubicadas a distancia menor que 2h de los apoyos.

En todas esas zonas, el comportamiento de la secciones transversales no verifica las hipótesis de Bernoulli. Por otra parte bajo tensiones relativamente bajas se produce fisuración del hormigón que deja de comportarse como medio continuo.

En esos casos se puede utilizar el modelo de reticulado de Morsch, e imaginar la viga trabajando como un reticulado con bielas de compresión, aportadas por el hormigón, y bielas de tracción, conformadas por la armadura.

Para el dimensionamiento de estas vigas la ACI 318 proporciona un procedimiento simplificado:

En lugar de colocar las armaduras mínimas indicadas en ese procedimiento simplificado, se puede calcular la armadura necesaria utilizando un modelo de bielas.

Para ello hay que trazar un conjunto de bielas que, formando un reticulado, transmitan las cargas hasta los apoyos. Este trazado no es único: pueden dibujarse distintos reticulados que sirvan a tal efecto. De ellos la estructura utilizar a aquel que le represente movilizar menor cantidad de energía.

En la figura 10 se muestra un ejemplo sencillo.

Para trazar el reticulado se adopta el ancho de las bielas y en función de esas dimensiones se tendrán las longitudes de bielas y sus ángulos. Resuelto estáticamente el reticulado se obtienen

Figura 10: Modelo de bielas

los esfuerzos en las bielas y se verifican las tensiones en cada una. Si fuese necesario se modifican las dimensiones asumidas para las bielas y se rehace el cálculo.

Debe colocarse la armadura necesaria para cubrir la tracción en las bielas traccionadas. Las tensiones en bielas comprimidas, debe verificarse que sean resistidas por el hormigón.

Para un puntal se verifica:

donde Fu es la carga mayorada en ese puntal calculada al resolver el reticulado; ‑ es el factor de reducción de resistencia; y Fn la resistencia nominal de la biela.

La resistencia se verifica para las bielas comprimidas, para las traccionadas, y para la zona del nudo (zona nodal).

La resistencia de un puntal sin armadura es:

Esta resistencia debe evaluarse en ambos extremos del puntal y tomar la menor de ambas. En la formula Ac es el área de la sección transversal del puntal, en el extremo considerado, y

siendo f’c la resistencia a compresión especificada del hormigón, y  β s un factor que tiene en cuenta la forma del puntal:  β s = 1 para puntales con sección constante;  β s = 0;75 o  β s = 0;60 para puntales con forma de "botella"; etc.

Las zonas nodales deben ser verificadas

donde An es el área de la sección del nodo perpendicular a la recta de acción de Fu; y la resistencia efectiva del hormigón en la zona nodal:

donde  β n = 1 si al nodo solo llegan bielas comprimidas;  β n = 0;8 si llega un tensor; y βn = 0;6 si llegan 2 o mas tensores.

Vigas - Tensiones de Compresión.

Las tensiones de compresión deben ser menores que 

. Esto se da si en el apoyo, la presión de apoyo no supera el valor:

Para el cálculo de la presión p se divide la reacción en el apoyo por el espesor de la viga y un ancho del apoyo en la dirección de la viga que no debe superar el 20% de la luz libre de la viga.

Para el cálculo de la presión p se divide la reacción en el apoyo por el espesor de la viga y un ancho del apoyo en la direccion de la viga que no debe superar el 20% de la luz libre de la viga.

Si hubiese refuerzos de borde (costillas) o si la viga esta indirectamente apoyada a través de placas transversales, debe verificarse que el esfuerzo de corte en el apoyo no supere el valor:

donde b es el espesor de la viga. Si L > h se reemplaza L por h en esta formula.